前言：昨天第一场团队赛看到的一个算是可能是裸的算法题吧，顺便就来学一下

首先我们都知道这个定理：
$$ 不共线的三个点确定一个圆 $$

所以说，我们只要知道三个点的坐标，就能求出这三个点所唯一确定的一个圆，使得这三个点都在圆上

那么，可列方程：

$$ (x - x_1)^2 + (y - y_1)^2 = r^2 \\\\ (x - x_2)^2 + (y - y_2)^2 = r^2 \\\\ (x - x_3)^2 + (y - y_3)^2 = r^2 $$

完全平方式展开得
$$ x^2-2x_1x+x_1^2 + y^2 - 2y_1y + y_1^2 = r^2 ①\\\\ x^2-2x_2x+x_2^2 + y^2 - 2y_2y + y_2^2 = r^2 ②\\\\ x^2-2x_3x+x_3^2 + y^2 - 2y_3y + y_3^2 = r^2 ③ $$
② - ①可得：

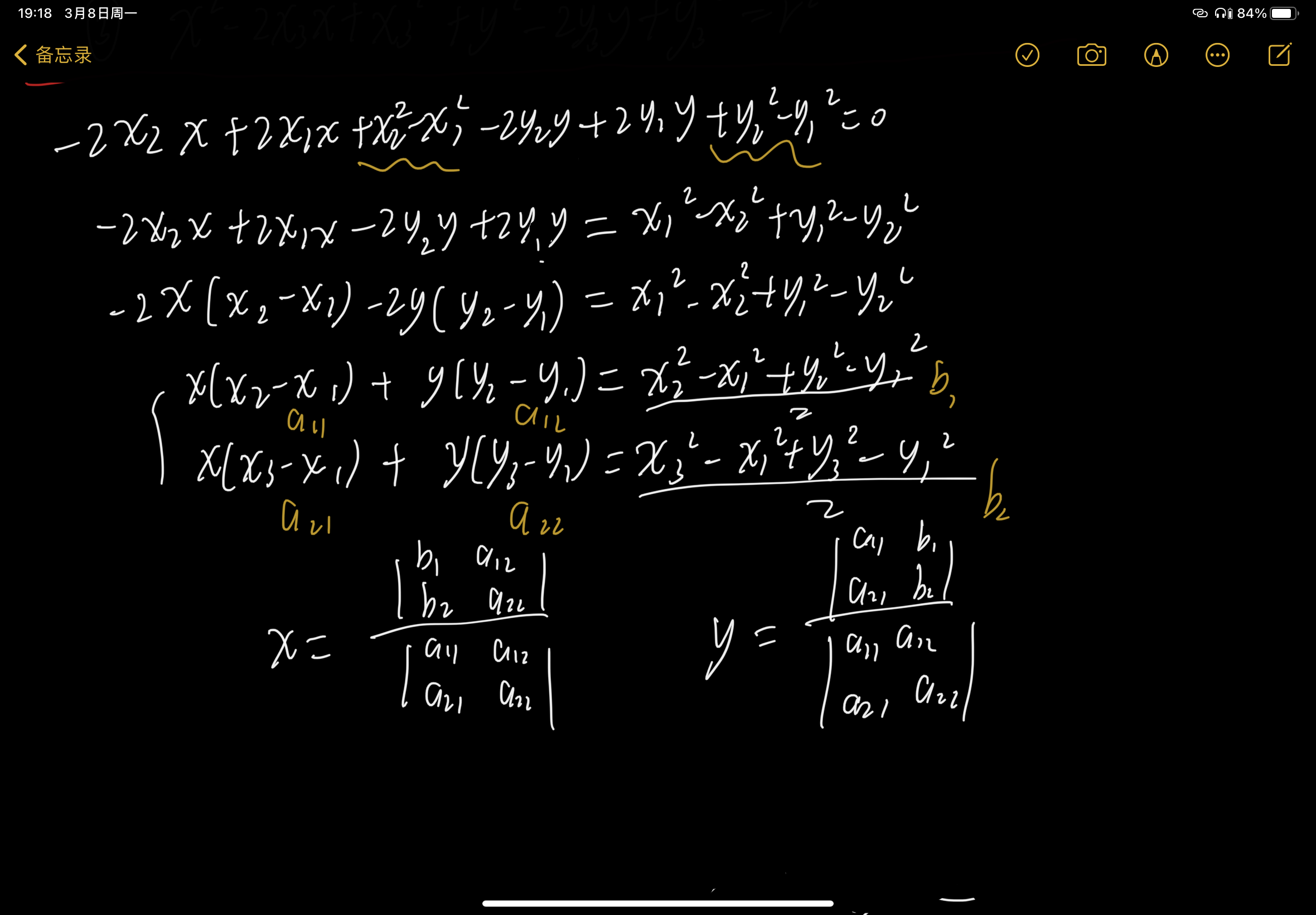
经过化简类别，就能得到③ - ①的式子（大括号第二个）

根据行列式解二元一次方程组的性质，我们就能确定这个圆的圆心的坐标是多少了（不会也可以解，只不过可以直接套行列式）

说这个算法的名字实际上用到的叫做随机增量法（打乱原数组顺序），我也不大懂，就是能降低复杂度

然后就是从第一个点开始作为初始圆，圆心就是这个点（姑且叫做a[1]），然后依次向后枚举（a[i]），如果下一个点在当前已知的圆的内部，我们就继续枚举下一个点；而如果此时这个点在当前圆的外部，我们就要重新设置一个新的圆了

枚举i前面的点j，如果此时两个点以他们的连线的中点作为圆心，两点连线作为直径，继续枚举j前面的点k，如果此时k在此时的圆外，那么i，j，k三个点组成的圆就是目前的最优解

简易证明：我们取一二个点,和第四个点进行三点定圆. 因为第四个点不在前三个点的圆中.所以第四个点定的新圆一定比前三个定的圆大.

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#define pf(x) (x) * (x)
#define eps 1e-12

using namespace std;

int n;
struct point{
    double x;
    double y;
}o, a[100000 + 10];

double r;

double dis(point a, point b){
    return sqrt(pf(a.x - b.x) + pf(a.y - b.y));
}

void get(point a, point b, point c){ //方程的计算
    double a11 = b.x - a.x;
    double a12 = b.y - a.y;
    double b1 = (pf(b.x) - pf(a.x) + pf(b.y) - pf(a.y)) * 0.5;
    double a21 = c.x - a.x;
    double a22 = c.y - a.y;
    double b2 = (pf(c.x) - pf(a.x) + pf(c.y) - pf(a.y)) * 0.5;

    o.x = (b1 * a22 - a12 * b2) / (a11 * a22 - a12 * a21);
    o.y = (a11 * b2 - b1 * a21) / (a11 * a22 - a12 * a21);
    r = dis(o, a);
}

int main(){
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i].x >> a[i].y;
    }
    random_shuffle(a + 1, a + 1 + n);
    o = a[1];
    r = 0;
    for(int i = 2; i <= n; i++){ //模拟那个过程
        if(dis(a[i], o) > r + eps){
            o = a[i];
            r = 0;
            for(int j = 1; j <= i - 1; j++){
                if(dis(a[j], o) > r + eps){
                    o.x = (a[i].x + a[j].x) / 2;
                    o.y = (a[i].y + a[j].y) / 2;
                    r = dis(o, a[j]);
                    for(int k = 1; k <= j - 1; k++){
                        if(dis(a[k], o) > r + eps){
                            get(a[i], a[j], a[k]);
                        }
                    }   
                }
            }
        }
    }
    printf("%.10lf\n%.10lf %.10lf", r, o.x, o.y);
    return 0;
}