题目描述

原题

维护一个字符串集合，支持两种操作：

“I x”向集合中插入一个字符串x；
“Q x”询问一个字符串在集合中出现了多少次。
共有N个操作，输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式
第一行包含整数N，表示操作数。

接下来N行，每行包含一个操作指令，指令为”I x”或”Q x”中的一种。

输出格式
对于每个询问指令”Q x”，都要输出一个整数作为结果，表示x在集合中出现的次数。

每个结果占一行。

数据范围
1≤N≤2∗104
输入样例：
5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：
1
0
1

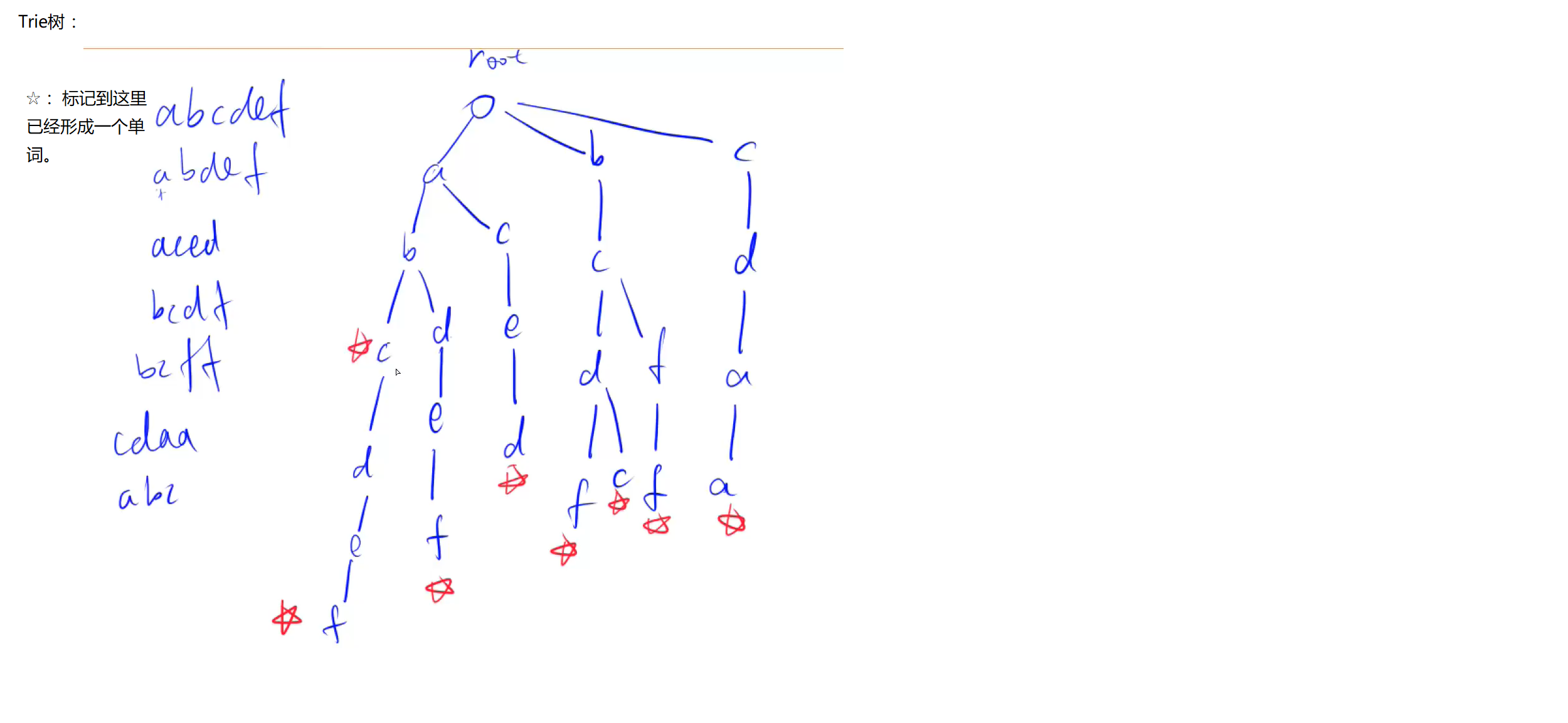
算法 Trie树

图解：

参考文献

y总讲解视频

C++ 代码

/*
Trie树  高效存储和查找字符串集合的数据结构
*/

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;
/*本题告诉我们只包含26个小写字母，所以每个子节点的个数是26
son 定义子节点的数组
cnt 存储的是以当前字母结尾的单词有多少个
idx 存的是当前用到的哪个下标。下标0的点既是根节点又是空节点（当一个点没有子节点
    的时候，我们让它也指向0）
*/
int son[N][26] , cnt[N] , idx ;
//要插入的字符串
char str[N];

//插入操作
void insert(char str[]){
    //从根节点开始
    int p = 0 ;
    /*这里是晚上找的资料：      a = "aad";
    string 并不是以‘\0'作为字符串结尾的标志，但是经试验，字符串可以越界
    访问a[3],并且字符串的结尾确实是'\0';*/
    //从前往后遍历，C++字符串结尾是\0 ,所以这里str[i]判断是不是走到结尾
    for(int i = 0 ; str[i] ; i++){
        //把a-z的字母映射成0-25的数字
        int  u = str[i] - 'a';
        //如果这个结点不存在，那就把他创造出来
        if(!son[p][u]) son[p][u] = ++idx;
        //指向这个结点
        p = son[p][u];

    }
    /*循环结束之后，p这个点对应的就是单词的最后一个字母。也就是说以这个字母结尾
    的单词又多了一个
    */
    cnt[p]++;
}


//查询操作
int query(char str[]){
    //还是从根节点开始
    int p = 0;
    //遍历
    for(int i = 0 ; str[i] ; i++ ){
        //获得字母对应的数字
        int u = str[i] - 'a';
        //这里是查询，如果不存在这个结点就直接返回0
        if(!son[p][u]) return 0;
        //指向这个子结点
        p = son[p][u];
    }
    //返回这个结点位置的单词数
    return cnt[p];
}

int main(){
    int n ; 
    scanf("%d" , &n);
    while(n--){
        //op一个单独的操作
        char op[2] ;
        //输入操作符  和字符串
        scanf("%s%s" , &op , &str);
        //如果操作符是插入就插入到str中
        if(op[0] == 'I') insert(str);
        //否则直接查询输出
        else printf("%d\n" , query(str));

    }
    return 0;
}