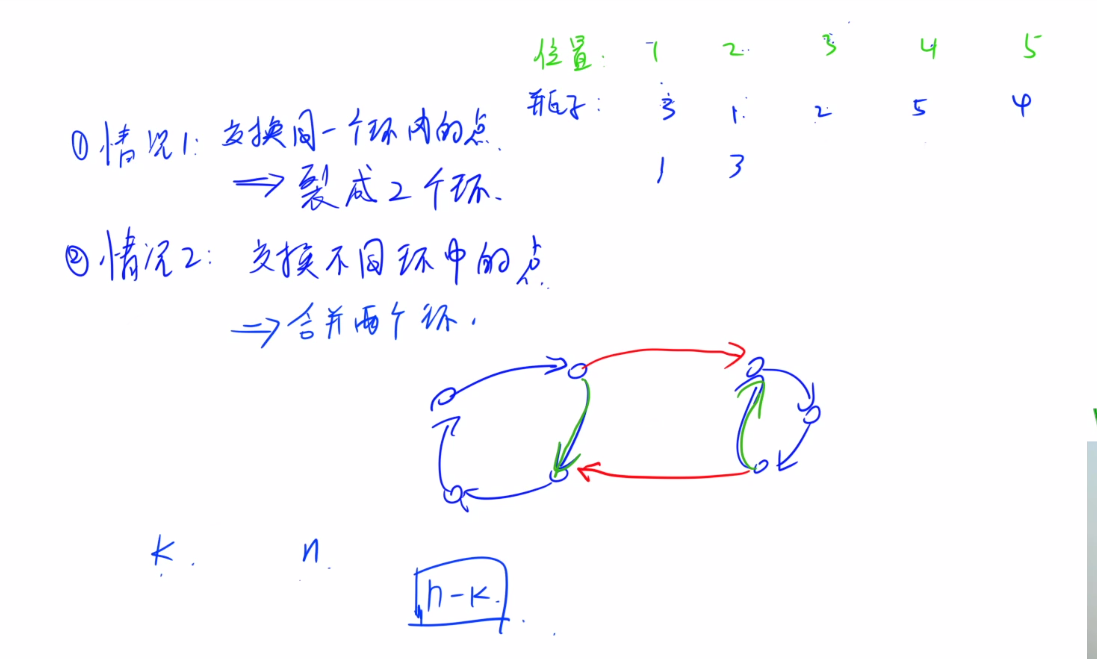
利用图的环数来计算

第一步:因为最终要把这一串数字变为顺序的，把当前的数(指向他应该在的位置下的数字)，比如3应该在第三个位置，第三个位置的数字是2，所以把3指向了2.
这里有一个性质离散数学的置换,交换两个数那么就可以裂开成两个环(增加一个环),最终的结果是每个数都应该指向自己，
总共要有n个环,如果现在有k个环，那么至少需要n - k 个操作，
所以我们需要找出按第一步操作的总环数再减去即可。

C++代码

#include<iostream>
#include<cstdio>
using namespace std;

const int N = 10010;
int a[N], st[N]; // st数组用来计算有多少个环的 
int n, cnt; // cnt是环数目的结果
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++){
        scanf("%d",&a[i]);
    }

    for(int i = 1;i <= n;i++){
        if(!st[i]){ // 当前元素未被标记
            cnt++;
            // 把所有环内的数标记完
            for(int j = i; !st[j]; j = a[j]){ // 一个箭头指向另一个箭头直到一个环内所以数都被标记为止
                st[j] = true;
            }
        }
    }

    printf("%d\n", n - cnt);
    return 0;
}

方法二：这是以前写的代码，循环遍历如果当前a[i]对应的数字不是i，那么把a[i]和a[a[i]]交换-->先把a[i]放到它应该在的位置上去,具体原因以后再补充，这可能是一种规律
#include<bits/stdc++.h>
using namespace std;
int a[10001];
long long  ans=0;
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }

    for(int i=1;i<=n;i++){
        while(a[i]!=i){
            swap(a[i],a[a[i]]);
            ans++;
        }
    }
    cout<<ans;
    return 0;
}