题目描述

现有一个加权无向连通图。给你一个正整数 n，表示图中有 n 个节点，并按从 1 到 n 给节点编号；另给你一个数组 edges，其中每个 edges[i] = [u_i, v_i, weight_i] 表示存在一条位于节点 u_i 和 v_i 之间的边，这条边的权重为 weight_i。

从节点 start 出发到节点 end 的路径是一个形如 [z_0, z_1, z_2, ..., z_k] 的节点序列，满足 z_0 = start、z_k = end 且在所有符合 0 <= i <= k-1 的节点 z_i 和 z_i+1 之间存在一条边。

路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(z_i) > distanceToLastNode(z_i+1) 的一条路径，其中 0 <= i <= k-1。

返回从节点 1 出发到节点 n 的 受限路径数。由于数字可能很大，请返回对 10^9 + 7 取余 的结果。

样例

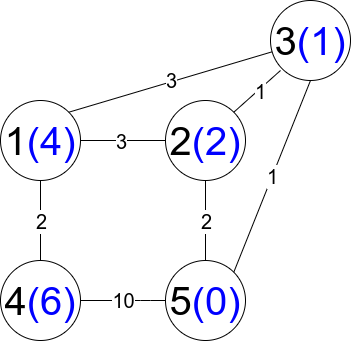
输入：n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
输出：3
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。
三条受限路径分别是：
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

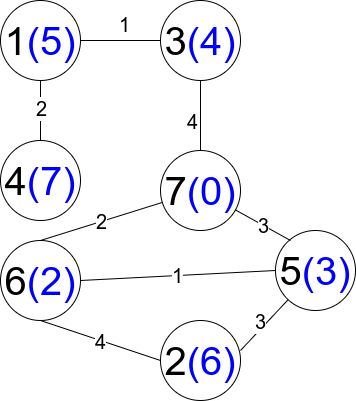
输入：n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
输出：1
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。
唯一一条受限路径是：1 --> 3 --> 7 。

限制

• 1 <= n <= 2 * 10^4
• n - 1 <= edges.length <= 4 * 10^4
• edges[i].length == 3
• 1 <= u_i, v_i <= n
• u_i != v_i
• 1 <= weight_i <= 10^5
• 任意两个节点之间至多存在一条边。
• 任意两个节点之间至少存在一条路径。

算法

(最短路，记忆化搜索) $O(n + km)$

1. 先求出 n 到各个节点的最短路，可以用 spfa 或者堆优化 dijkstra。
2. 从 1 号节点开始记忆化搜索，对于当前节点 u，可以从 v 节点进行转移，满足 dis[v] < dis[u]。递归出口为编号为 n 的节点。

时间复杂度

• spfa 求最短路的时间复杂度是 $O(n + km)，堆优化 dijkstra 的时间复杂度为 $O(n + m \log n)$。
• 记忆化搜索的时间复杂度为 $O(n + m)$。
• 故总时间复杂度为 $O(n + km)$ 或者 $O(n + m \log n)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储求最短路以及记忆化搜索的数据结构。

C++ 代码 1（spfa）

#define MOD 1000000007

class Solution {
private:
    // 记忆化搜索
    int solve(int u, int n, vector<int> &f, const vector<int> &dis,
              const vector<vector<pair<int, int>>> &graph) {

        if (f[u] != -1)
            return f[u];

        if (u == n - 1)
            return f[u] = 1;

        f[u] = 0;
        for (const auto &t : graph[u]) {
            int v = t.first;
            if (dis[v] < dis[u])
                f[u] = (f[u] + solve(v, n, f, dis, graph)) % MOD;
        }
        return f[u];
    }

public:
    int countRestrictedPaths(int n, vector<vector<int>>& edges) {
        vector<vector<pair<int, int>>> graph(n);
        for (const auto &e : edges) {
            int x = e[0] - 1, y = e[1] - 1, w = e[2];
            graph[x].emplace_back(y, w);
            graph[y].emplace_back(x, w);
        }

        // spfa 求最短路
        vector<int> dis(n, INT_MAX);
        vector<bool> vis(n, false);
        queue<int> q;
        vis[n - 1] = true;
        dis[n - 1] = 0;
        q.push(n - 1);

        while (!q.empty()) {
            int u = q.front();
            vis[u] = false;
            q.pop();
            for (const auto &t : graph[u]) {
                int v = t.first, w = t.second;
                if (dis[v] > dis[u] + w) {
                    dis[v] = dis[u] + w;
                    if (!vis[v]) {
                        q.push(v);
                        vis[v] = true;
                    }
                }
            }
        }

        vector<int> f(n, -1);
        return solve(0, n, f, dis, graph);
    }
};

C++ 代码 2（堆优化 dijkstra）

#define MOD 1000000007

struct Node {
    int x, d;
    Node(int x_, int d_):x(x_), d(d_){}

    bool operator < (const Node &p) const {
        return d > p.d;
    }
};

class Solution {
private:
    // 记忆化搜索
    int solve(int u, int n, vector<int> &f, const vector<int> &dis,
              const vector<vector<pair<int, int>>> &graph) {

        if (f[u] != -1)
            return f[u];

        if (u == n - 1)
            return f[u] = 1;

        f[u] = 0;
        for (const auto &t : graph[u]) {
            int v = t.first;
            if (dis[v] < dis[u])
                f[u] = (f[u] + solve(v, n, f, dis, graph)) % MOD;
        }
        return f[u];
    }

public:
    int countRestrictedPaths(int n, vector<vector<int>>& edges) {
        vector<vector<pair<int, int>>> graph(n);
        for (const auto &e : edges) {
            int x = e[0] - 1, y = e[1] - 1, w = e[2];
            graph[x].emplace_back(y, w);
            graph[y].emplace_back(x, w);
        }

        // 堆优化 dijkstra 求最短路
        vector<int> dis(n, INT_MAX);
        priority_queue<Node> q;

        dis[n - 1] = 0;
        q.push(Node(n - 1, 0));

        while (!q.empty()) {
            Node u = q.top();
            q.pop();

            for (const auto &t : graph[u.x]) {
                int v = t.first, w = t.second;
                if (dis[v] > dis[u.x] + w) {
                    dis[v] = dis[u.x] + w;
                    q.push(Node(v, dis[v]));
                }
            }
        }

        vector<int> f(n, -1);
        return solve(0, n, f, dis, graph);
    }
};