【题目描述】

AcWing 895. 最长上升子序列

【思路】

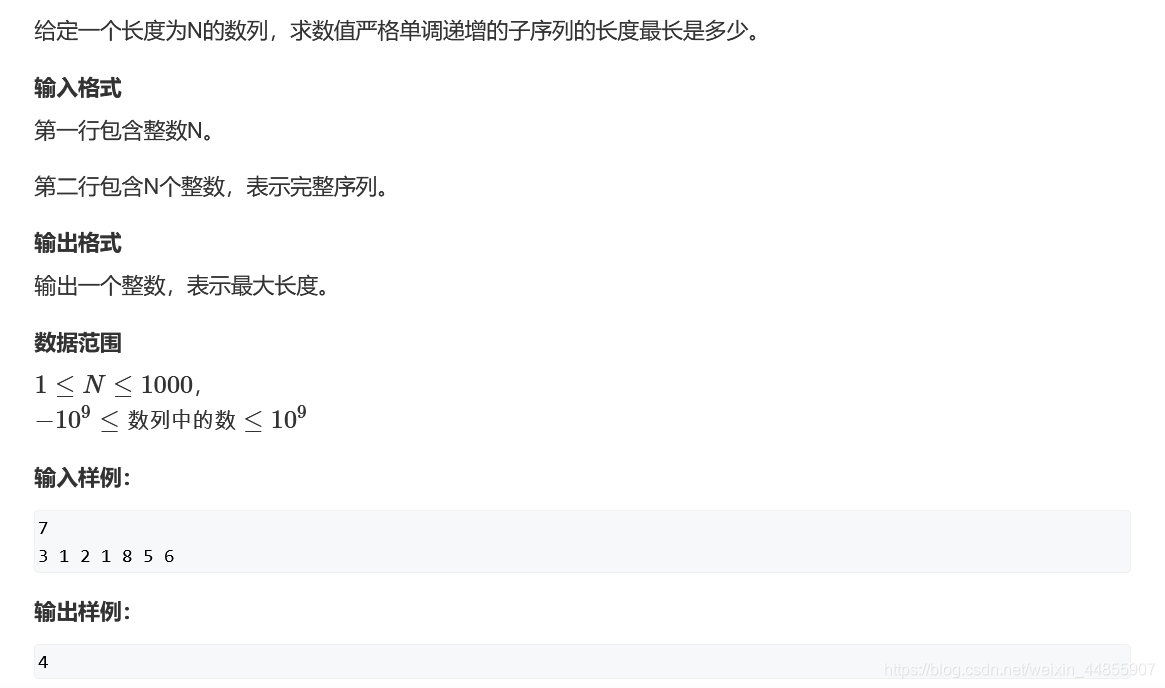
动态规划

7
3 1 2 1 8 5 6

原序列为 a，状态数组为f。
状态表示：
f[i]表示一个状态集合，该集合为所有以第i个元素结尾的上升子序列。例如f[4]，其上升子序列集合为{ {3,8},{1,8}, {2,8},{1,2,8} }。f[i]的属性值为集合元素的最大长度，表示以第i个元素结尾的最长上升子序列长度。

状态转移：
以第i - 1个数 是原序列的哪个数来划分f[i]状态表示的集合，第i - 1个数可以是原序列的第 0 、 1 …… i - 1。那么求出每一个元素，取长度的max。
f[i] = max(f[j]) , j = 0, 1……i - 1且a[i] > a[j]

/*
  3 1 2 1 8 5 6
0 1 1 2 2 3 3 4
1 2 5 6 
*/
import java.util.Scanner;
public class Main{
    static int N = 1010;
    static int a[] = new int[N]; //原序列
    static int f[] = new int[N]; //状态数组
    public static void main(String args[]){
        Scanner reader = new Scanner(System.in);
        int n = reader.nextInt();
        for(int i = 0; i < n; i ++) a[i] = reader.nextInt();

        //以第0个元素结尾的最长上升子序列长度为1
        f[0] = 1;
        for(int i = 0; i < n; i ++)
        {
            for(int j = 0; j < i; j ++)
            {
                if(a[i] > a[j]) f[i] = Math.max(f[i], f[j] + 1);
                else f[i] = Math.max(f[i], 1);

            }
        }
        int ans = f[0];
        for(int i = 1; i < n; i ++)
            if(f[i] > ans)
                ans = f[i];
        System.out.println(ans);
    }
}

DFS

TLE 只过了两个数据

import java.util.Scanner;
public class Main{
    static int N = 1010;
    static int f[] = new int[N];
    static int n, ans = Integer.MIN_VALUE;
    public static boolean check(int bestf[], int len){
        for(int i = 2; i <= len; i ++)//非严格递增序列
            if(bestf[i] <= bestf[i - 1]) return false;
        return true;
    }
    public static void dfs(int m, int len, int[]bestf){
        if( m == n){
            //递增序列 且长度大于ans则更新
            if(len > ans && check(bestf,len)) ans = len;
            return;
        }
        //第m个元素选
        bestf[len + 1] = f[m];
        dfs(m + 1, len + 1, bestf);

        //第m个元素不选
        dfs(m + 1, len, bestf);
    }
    public static void main(String args[]){
        Scanner reader = new Scanner(System.in);
        n = reader.nextInt();
        for(int i = 0; i < n; i ++) f[i] = reader.nextInt();
        int [] bestf = new int[n + 1];
        dfs(0, 0, bestf);
        System.out.println(ans);
    }
}