题目描述

给你一个无向图，无向图由整数 n，表示图中节点的数目，和 edges 组成，其中 edges[i] = [u_i, v_i] 表示 u_i 和 v_i 之间有一条无向边。同时给你一个代表查询的整数数组 queries。

第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目：

• a < b
• cnt 是与 a 或者 b 相连的边的数目，且 cnt 严格大于 queries[j]。

请你返回一个数组 answers，其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。

请注意，图中可能会有 重复边。

样例

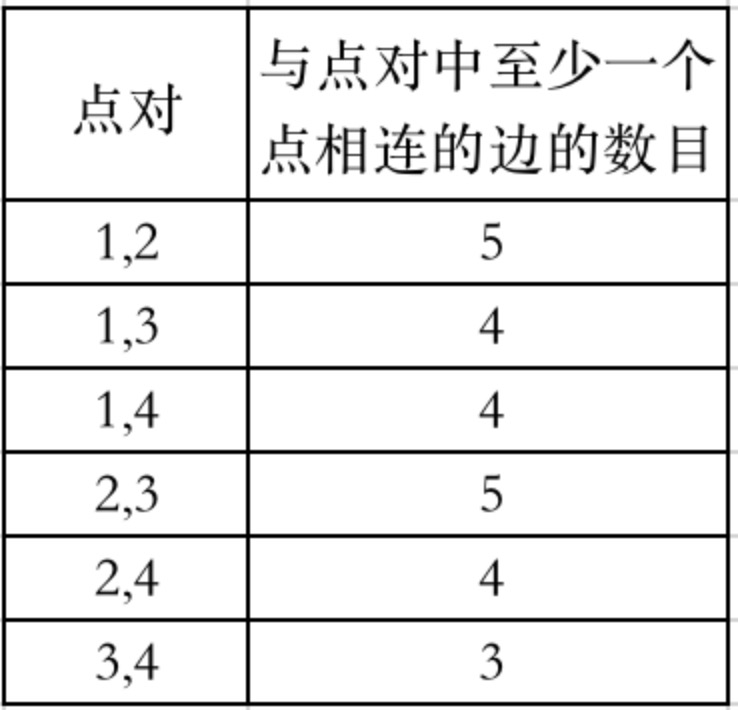
输入：
n = 4
edges = [[1,2],[2,4],[1,3],[2,3],[2,1]]
queries = [2,3]

输出：[6,5]

解释：每个点对中，与至少一个点相连的边的数目如上图所示。

输入：
n = 5,
edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]]
queries = [1,2,3,4,5]

输出：[10,10,9,8,6]

限制

• 2 <= n <= 2 * 10^4
• 1 <= edges.length <= 10^5
• 1 <= u_i, v_i <= n
• u_i != v_i
• 1 <= queries.length <= 20
• 0 <= queries[j] < edges.length

算法

(双指针) $O(n \log n + m \log m + q(n + m))$

1. 求出每个点的度数，并将度数从小到大排序。
2. 对于每个询问，我们计算出不符合要求的点对的数量，然后用总点对数量减去这个数字就是答案。
3. 首先，在排序后的度数数组上应用双指针，求出两数之和小于等于 $q$ 的数量。
4. 但剩下的并不一定都是符合要求的，因为对于每条边的两个端点，其度数之和发生了重复计算，所以接下来我们通过遍历边集数组，来进一步排除掉不符合要求的数对。
5. 对于边 (x, y)，如果 d(x) + d(y) > q 且 d(x) + d(y) - dup <= q，则说明这个数对应当额外被排除，其中 dup 表示边 (x, y) 重复出现的次数。可以通过先排序预处理边集数组来方便的求出每条边的 dup。

时间复杂度

• 预处理的时间复杂度为 $O(n \log n + m \log m)$。
• 对于每个询问，需要 $O(n + m)$ 的时间求解。
• 故总时间复杂度为 $O(n \log n + m \log m + q(n + m))$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储度数数组和答案。

C++ 代码

class Solution {
public:
    vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {
        const int m = edges.size();
        vector<int> deg(n, 0), c(n, 0);
        for (const auto &e : edges) {
            int x = e[0] - 1, y = e[1] - 1;
            deg[x]++; c[x]++;
            deg[y]++; c[y]++;
        }
        sort(c.begin(), c.end());

        for (int i = 0; i < edges.size(); i++)
            if (edges[i][0] > edges[i][1])
                swap(edges[i][0], edges[i][1]);

        sort(edges.begin(), edges.end());

        vector<int> ans;
        for (int q : queries) {
            int res = n * (n - 1) / 2;
            int l = 0, r = n - 1;
            while (l < r) {
                if (c[l] + c[r] <= q) {
                    res -= r - l;
                    l++;
                } else {
                    r--;
                }
            }

            int dup = 1;
            for (int i = 0; i < m; i++) {
                if (i < m - 1 && edges[i] == edges[i + 1]) {
                    dup++;
                    continue;
                }
                int x = edges[i][0] - 1, y = edges[i][1] - 1;
                if (deg[x] + deg[y] > q && deg[x] + deg[y] - dup <= q)
                    res--;

                dup = 1;
            }
            ans.push_back(res);
        }
        return ans;
    }
};