题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

$1≤n,m≤1000$

$1≤q≤100000$

$1≤x1≤x2≤n$

$1≤y1≤y2≤m$

$−1000≤c≤1000$

$−1000≤矩阵内元素的值≤1000$

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

思路

（注：下文中所提到的“面积”所指的是当前矩阵所有格子的数值之和）

实际上和一维的差分没有太大的区别

详细可见AcWing 797. 差分

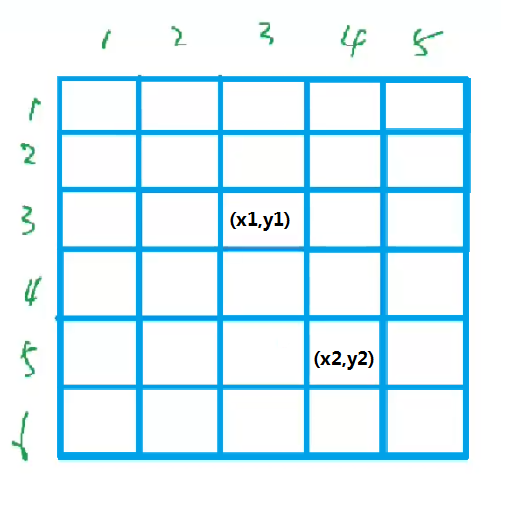
现在我们要求从(x1,y1)到(x2,y2)的矩阵的面积，即红色的部分

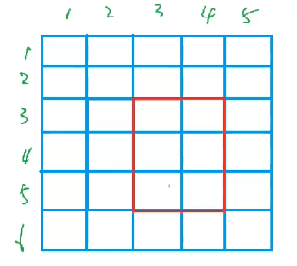
我们把b[x1][y1]加上c，就相当于把所有含有b[x1][y1]这个格子的前缀和（即图中肉色的部分）都加上了c

这一步就是b[x1][y1]+=c

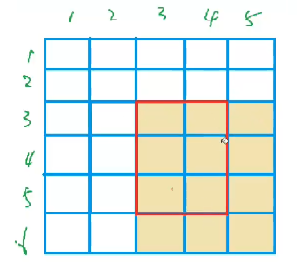
然后我们把b[x1][y2+1]减去c，就相当于把所有含有b[x1][y2+1]这个格子的前缀和（即图中由肉色变为白色的部分）都减去了c

这一步就是b[x1][y2+1]-=c

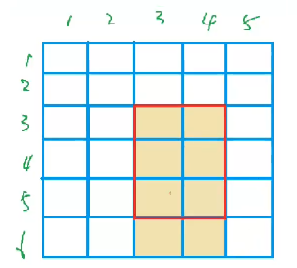
同理，我们把b[x2+1][y1]减去c，就相当于把所有含有b[x2+1][y1]这个格子的前缀和（即图中再次由肉色变为白色的部分和由白色变为黑色的部分）都减去了c

这一步就是b[x2+1][y1]-=c

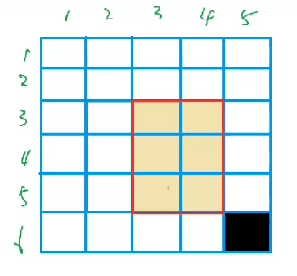
再上图中我们发现b[x2+1][y2+1]这个格子被减去了两次，被标记为黑色，而我们只想减去一次，所以我们还要再加上一次

我们把b[x2+1][y2+1]加上c，就相当于把所有含有b[x2+1][y2+1]这个格子的前缀和（即图中黑色的部分）都加上了c

这一步就是b[x2+1][y2+1]+=c

最后我们的图就会变成

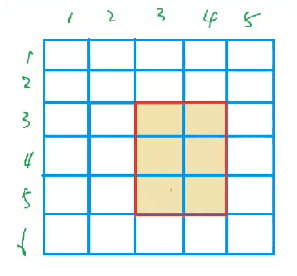
就只有红色的部分加上了c，完成此题目

代码

#include<iostream>
using namespace std;
int n,m,q,l,r,c;
int a[1010][1010],b[1010][1010];
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>a[i][j];
            insert(i,j,i,j,a[i][j]);
        }
    }
    int x1,y1,x2,y2,c;
    while(q--)
    {
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
            cout<<b[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

附：二维差分 —— 模板题 AcWing 798. 差分矩阵

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c