题目描述
输入一个长度为$n$的整数序列。
接下来输入$m$个操作,每个操作包含三个整数$l$, $r$, $c$,表示将序列中$[l, r]$之间的每个数加上$c$。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数$n$和$m$。
第二行包含$n$个整数,表示整数序列。
接下来$m$行,每行包含三个整数$l$,$r$,$c$,表示一个操作。
输出格式
共一行,包含$n$个整数,表示最终序列。
数据范围
$1≤n,m≤100000$
$1≤l≤r≤n$
$−1000≤c≤1000$
$−1000≤整数序列中元素的值≤1000$
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
思路
差分就是前缀和的逆运算
差分就是:
给定一个数组a
然后自己构造一个b数组
使a数组是b数组的前缀和
构造的方法也很简单:
b1=a1
b2=a2-a1
b3=a3-a2
……
bn=an-an-1
原因就是:
当b1=a1,b2=a2-a1时
b1+b2=a1+(a2-a1)=a2
当b1=a1,b2=a2-a1,b3=a3-a2时
b1+b2+b3=a1+(a2-a1)+(a3-a2)=a3
以此类推
但是!以上只作了解,在差分中并不是特别重要,我们要做的就是先想象一个这样的$b$数组,假定$a$数组全部都为$0$,那么$b$数组也都是$0$
$b$数组就是为了我们可以在$O(n)$的时间复杂度中求出$a$数组
这道题的题意是让我们把从a[l]到a[r]依次加上$c$
如果我们用暴力枚举的方法的话,就要循环一遍,时间复杂度是$O(n)$
但如果我们用差分的方法来做的话,时间复杂度就是$O(1)$
刚才我们提到了,$a$数组是$b$数组的前缀和,我们可以用b数组来求出a数组
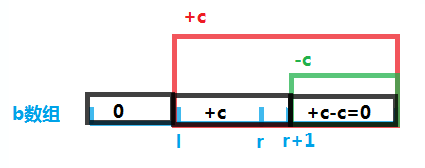
如果我们要把a[l]到a[r]的每一个数都加上c的话,我们直接把b[l]加上c就行了
因为a[l]=b[1]|b[2]+……+b[l],a[l+1]=b[1]|b[2]+……+b[l+1]……每一个在a[l]之后的数都会加上$c$
但正因如此,a[r]之后的数也会加上$c$
但是a[r]之后的数不能加上$c$
只要把b[r-1]减去$c$就行了
理由同上
因为a[r+1]=b[1]|b[2]+……+b[r+1],a[r+2]=b[1]|b[2]+……+b[l+2]……每一个在a[r+1]之后的数都会减去$c$
注意:在这里是a[r+1]因为在加上$c$的时候包括a[r],所以a[r]不用减去$c$
在a[l]之后的数都加上了$c$,在a[r+1]后面的都减去了$c$,所以实际上在a[r+1]后面的数加上了$c$又减了$c$,没有变
这样就可以保证从a[l]到a[r]的每一个数都加上了$c$
代码
AC代码
#include<iostream>
using namespace std;
int n,m,l,r,c;
int a[100010],b[100010];
void insert(int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
insert(i,i,a[i]);
}
while(m--)
{
cin>>l>>r>>c;
insert(l,r,c);
}
for(int i=1;i<=n;i++)
{
b[i]+=b[i-1];
}
for(int i=1;i<=n;i++)
{
cout<<b[i]<<" ";
}
return 0;
}
TLE代码
#include<iostream>
using namespace std;
int l,r,c;
int n,m;
int a[100010];
int b[100010];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
b[i]=a[i]-a[i-1];
}
for(int i=1;i<=n;i++)
{
a[i]=0;
}
while(m--)
{
cin>>l>>r>>c;
b[l]+=c;
b[r+1]-=c;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
a[i]+=b[j];
}
cout<<a[i]<<' ';
}
return 0;
}
TLE代码是我自己写的,就直接按照我所说的思路进行了模拟
显然行不通……
之后了解了y总的代码
里面巧妙的运用了一个函数
这个函数在输入之后,就直接把a数组的每一个元素进行差分,然后放进了b数组
当然也可以理解成b[i]=a[i]-a[i-1]
因为在进入函数之后,b[i+1]-=a[i]
因为a数组的初始化为0
所以b[i-1]实际上为0-a[i]
在下一次进入函数的时候,在当前状态就意味着a[i]=0-a[i-1]+a[i]即b[i]=a[i]-a[i-1]
附:一维差分 —— 模板题 AcWing 797. 差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c

