题目描述

维护一个集合，支持如下几种操作：

“I x”，插入一个数x；
“Q x”，询问数x是否在集合中出现过；
现在要进行N次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数N，表示操作数量。

接下来N行，每行包含一个操作指令，操作指令为”I x”，”Q x”中的一种。

输出格式
对于每个询问指令“Q x”，输出一个询问结果，如果x在集合中出现过，则输出“Yes”，否则输出“No”。

每个结果占一行。

数据范围
1≤N≤10^5
−10^9≤x≤10^9

样例

输入样例：
5
I 1
I 2
I 3
Q 2
Q 5
输出样例：
Yes
No

算法1

拉链法

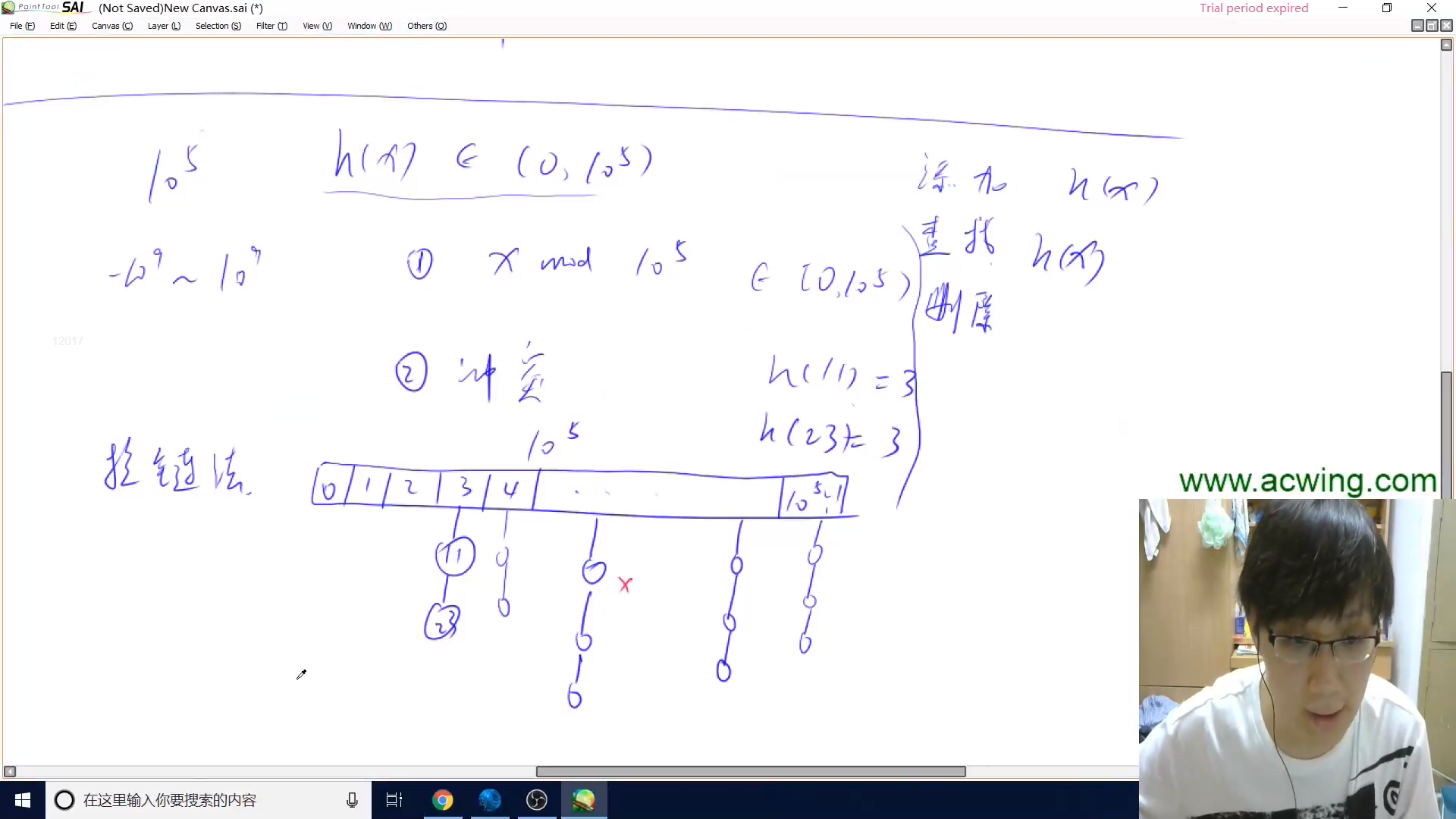
python 代码

#拉链法
#哈希表
#1.存储结构：
#开放寻址法
#拉链法
#哈希函数，把x映射到1-N之间的数。
#N取大于100000的最小的质数
def insert(x):
    global idx
    k=(x%N+N)%N     #余数为正数
    e[idx]=x
    ne[idx] = h[k]
    h[k]=idx
    idx+=1

def find(x):
    k=(x%N+N)%N
    i=h[k]
    while i!=-1:
        if e[i]==x:
            return True
        i=ne[i]
    return False


if __name__ == "__main__":
    N = 100003
    h = [-1 for _ in range(N)]      #拉出来的链，单链表结构
    e = [0]*N
    ne = [0]*N
    idx=0
    n=int(input())
    for i in range(n):
        op=input().split()
        if op[0]=="I":
            insert(int(op[1]))
        else:
            if find(int(op[1])):
                print("Yes")
            else:
                print("No")

算法

开放寻址法

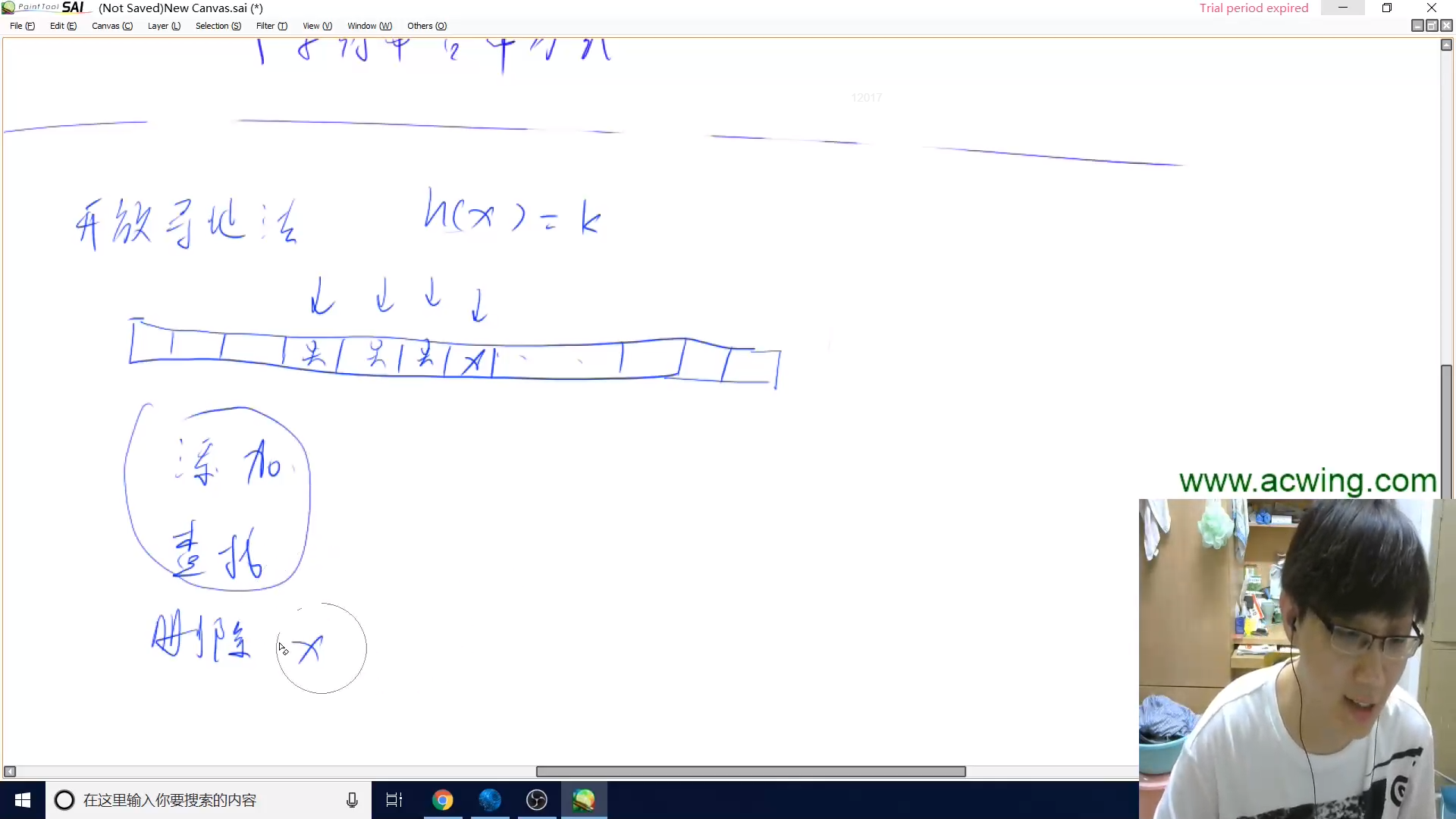
python 代码

#开放寻址法
#不用单链表，开一个数组，范围开到题目范围的2~3倍
def find(x):
    k=(x%N+N)%N
    while h[k]!=null and h[k]!=x:       #不等于x说明当前位置有人了
        k+=1
        if k==N:        #k已经遍历到最后一个位置，就要从头开始遍历
            k=0
    return k            #如果x在哈希表中，k就是x的下标。如果不在哈希表中，k就是x应该存储的位置


if __name__ == "__main__":
    n = int(input())
    N = 200003
    null = 0x3f3f3f3f3f       #大于1e9的数，
    h=[null]*N
    for i in range(n):
        op=input().split()
        x=int(op[1])
        k=find(x)
        if op[0]=="I":
            h[k]=x
        else:
            if h[k]==null:
                print("No")
            else:
                print("Yes")