题目描述

在一个数组中除了一个数字只出现一次之外，其他数字都出现了三次。

请找出那个只出现一次的数字。

你可以假设满足条件的数字一定存在。

思考题：

• 如果要求只使用 O(n) 的时间和额外 O(1) 的空间，该怎么做呢？

样例

输入：[1,1,1,2,2,2,3,4,4,4]

输出：3

算法1

(位运算) $O(32n) $

枚举每个数的每一位，用 one 记录每一位 1 出现的个数，如果 one % 3 == 1 说明答案中的当前位是 1，否则 one % 3 == 0 说明答案中的当前位不是 1，只有这两种情况，因为剩下的数都出现了三次，只有答案是出现一次的数字，所以处理完每一位之后就可以得到答案
比较好理解

时间复杂度

枚举数字的每一位，每个数字 32 位，总共 n 个数，所以时间复杂度为 $O(32n)$，但这个算法其实不是 $O(n)$ 的，假设 n 的范围是 $10^6$，则 $ logn < 32 $，所以此算法时间复杂度是大于 $O(nlogn)$ 的。

C++ 代码

class Solution {
public:
    int findNumberAppearingOnce(vector<int>& nums) {
        int res = 0;
        for (int i = 0; i < 32; i ++ )
        {
            int one = 0;
            for (auto x : nums)
                if (x >> i & 1) one ++ ;

            if (one % 3 == 1) res += 1 << i; 
        }
        return res;
    }
};

算法2

(位运算 + 有限状态自动机) $O(n)$

初始状态 (ones, twos) = (0, 0) 遇到 1 转移到下一个状态，遇到 0 就是自环
对所有数处理完之后，ones 中存的就是那个唯一只出现一次的数字

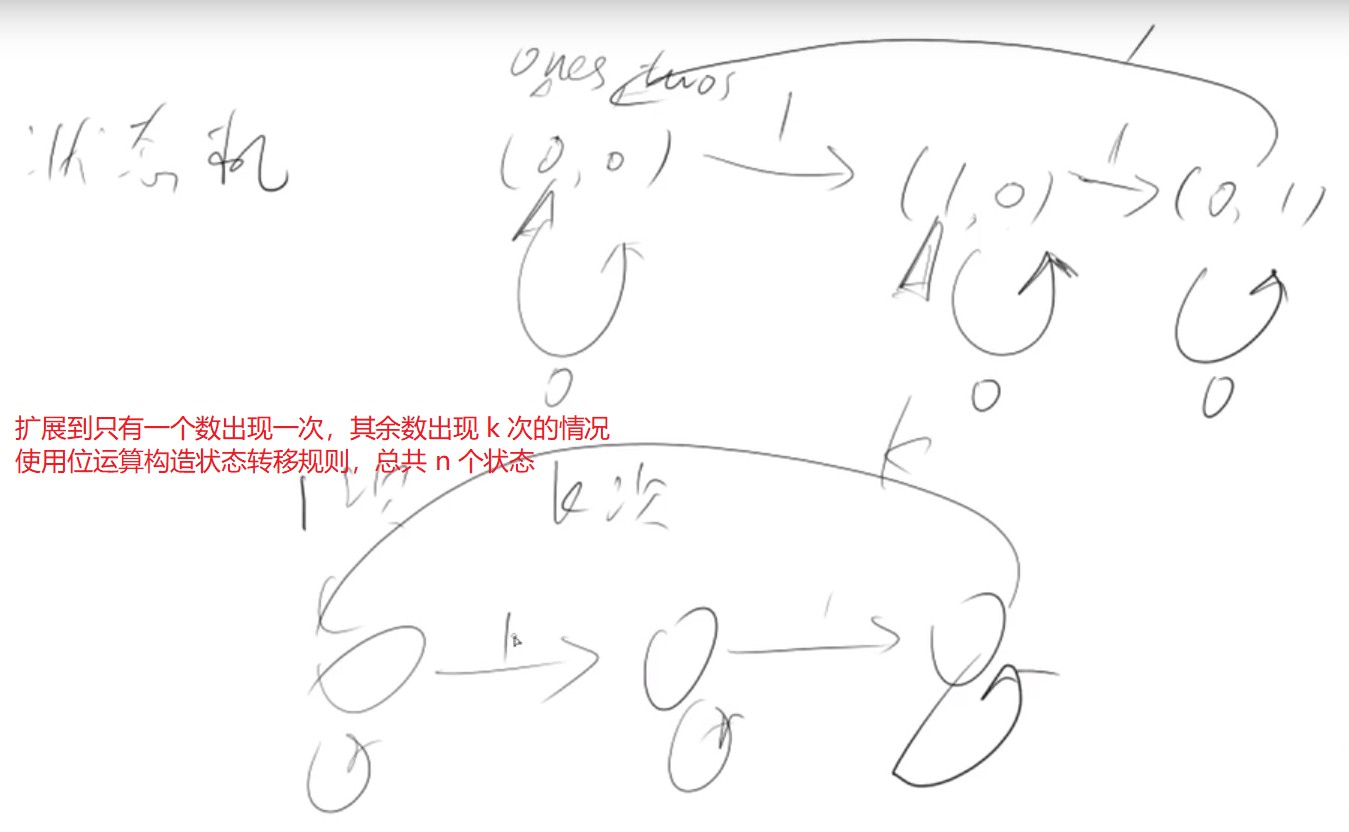
太巧妙了，思维跳跃性较强

时间复杂度

迭代 n 次，时间复杂度为 $O(n)$

C++ 代码

class Solution {
public:
    int findNumberAppearingOnce(vector<int>& nums) {
        int ones = 0, twos = 0;
        for (auto x : nums)
        {
            ones = (ones ^ x) & ~twos;
            twos = (twos ^ x) & ~ones;
        }
        return ones;
    }
};