题目描述

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。
如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

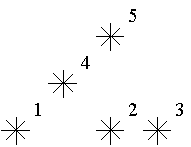
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1级的。
例图中有 1个 0 级，2 个 1 级，1 个 2 级，1 个 3级的星星。
给定星星的位置，输出各级星星的数目。换句话说，给定N个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式
第一行一个整数 N，表示星星的数目；
接下来 N行给出每颗星星的坐标，坐标用两个整数 x,y表示；不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x坐标增序给出。

输出格式
N行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1级的星星的数目。

数据范围
1≤N≤15000,
0≤x,y≤32000

样例

输入样例：

5
1 1
5 1
7 1
3 3
5 5
输出样例：

1
2
1
1
0

• 求一个星星的等级，就是要求出横纵坐标均小于这个行的坐标的星星的个数，由于输入是按照纵坐标从小到大的顺序，如果纵坐标相等，则按横坐标从小到大输入，所以当输入一个坐标时，纵坐标一定大于前面的所有的坐标，我们只需看前面输入的坐标有多少个横坐标小于此横坐标的 即可。
• 题目要求求某一个点(x,y)左下方星星的个数(不包括自己)，且星星按y坐标增序给出，y 坐标相同的按x坐标增序给出,因此对于每个新来的点(x,y),y是当前纵坐标的最大值，只需要求[1,x]中星星出现的数量即可，前缀和。
  *需要考虑两个问题：
  1.A[x]+1,(横坐标为x的星星个数 + 1),代码实现：add(x,1),将当前判断的这个点更新到树状数组里面去
  2.A[1 ~ x],求前缀和,求横坐标 1 ~ x 中星星出现的数量即可

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
int x,y; 
int num[15005];//等级为i的星星的个数 
int tr[32005];//树状数组
int a[32005];//横坐标为i的星星的个数 
int lowbit(int x){
    return x & -x;
}
//x位置上+v,更新tr[]数组 
void add(int x,int v){
    for(int i=x;i<32005;i+=lowbit(i)){
        tr[i]+=v;
    }
}
//前缀和  
int query(int x){
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}
int main(int argc, char** argv) {
   scanf("%d",&n);
   for(int i=0;i<n;i++){
    scanf("%d%d",&x,&y);
    x++;
    num[query(x)]++;//等级就是横坐标 1 ~ x 中星星出现的数量,等级为[]的星星个数+1 
    add(x,1);  //将当前判断的这个点更新到树状数组里面去 
   } 
   for(int i=0;i<n;i++){
    printf("%d\n",num[i]);
   }
    return 0;
}