题目描述

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b]的连续和。

输入格式
第一行包含两个整数 n和 m，分别表示数的个数和操作次数。
第二行包含 n个整数，表示完整数列。
接下来 m行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。
数列从 1开始计数。

输出格式
输出若干行数字，表示 k=0时，对应的子数列 [a,b]的连续和。

数据范围
1≤n≤100000,
1≤m≤100000，
1≤a≤b≤n

样例

输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：
11
30
35

树状数组：

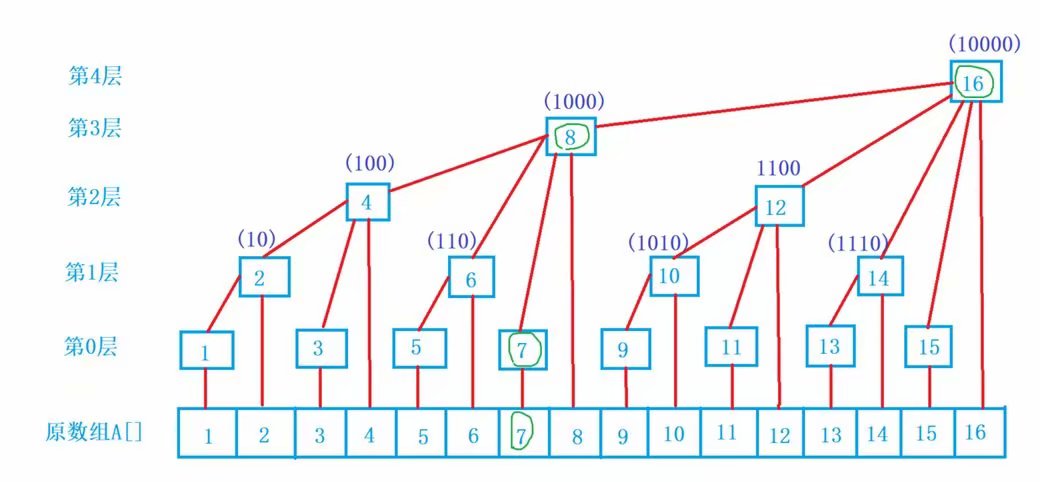
C[1]=A[1]
C[2]=C[1]+A[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[4]+C[3]+C[2]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[6]+C[5]=A[5]+A[6]
C[7]=A[7]
C[8]=A[8]+C[7]+C[6]+C[4]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
.............

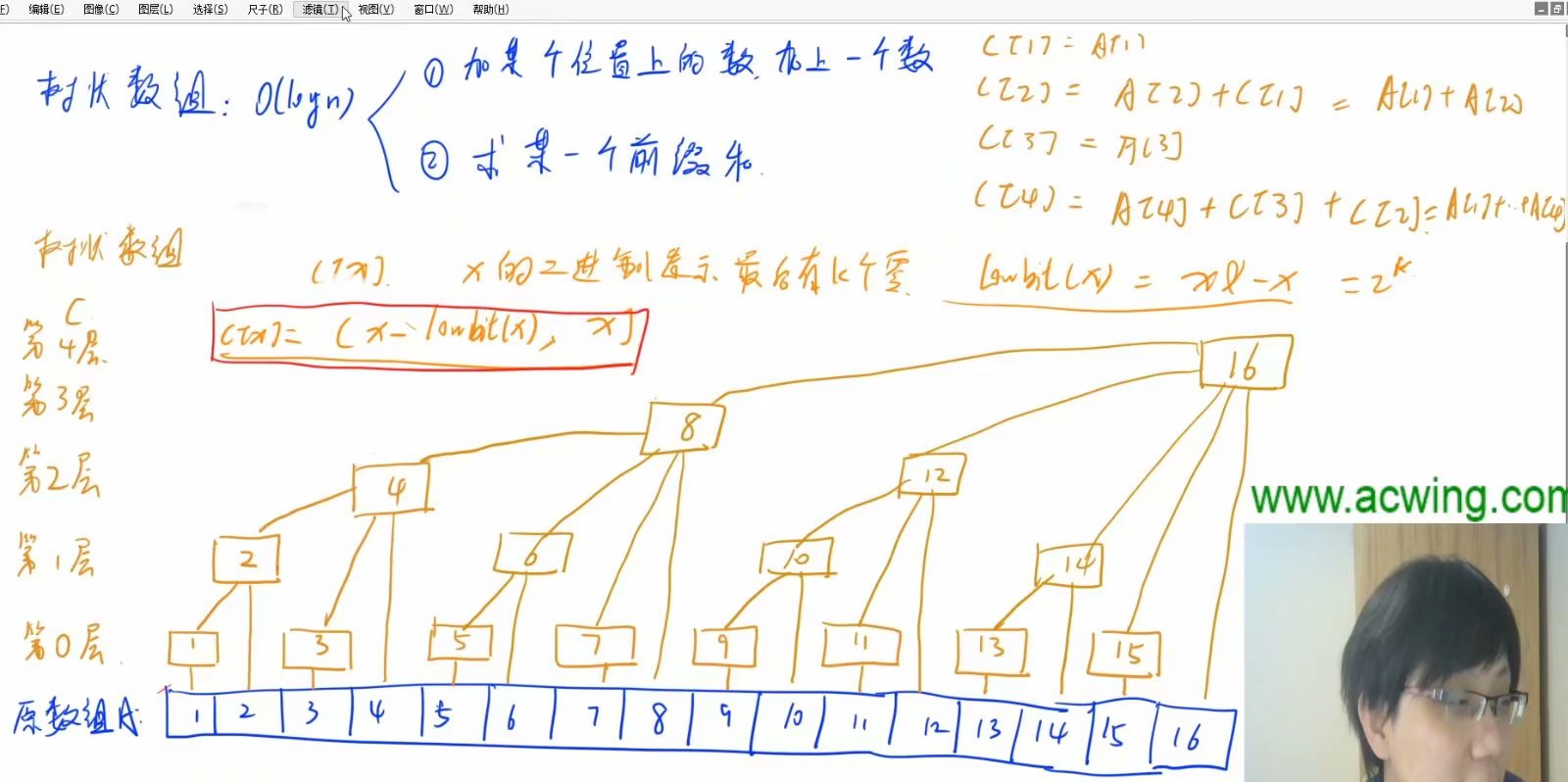
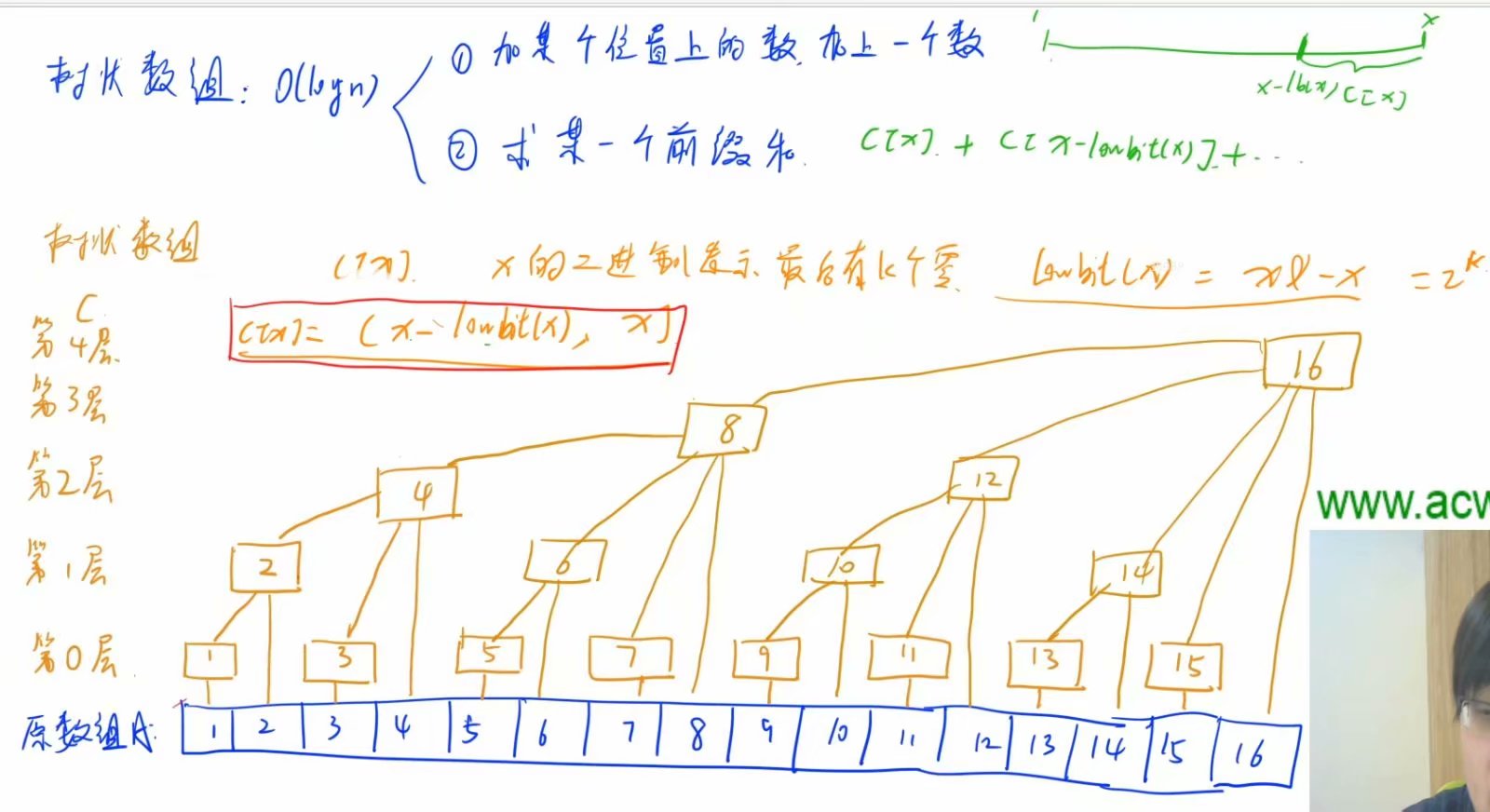
C[x]: x的二进制末尾0的个数k表示x在第k层

C[x]=(x-2^k , x] = (x - lowbit(x) , x] ，(该区域的和)注意这里不包括左边界，包括右边界，左开右闭

树状数组牢记三个函数：

//求2^k, k指x的二进制末尾0的个数k表示x在第k层

int lowbit(int x){
    return x & -x;
}

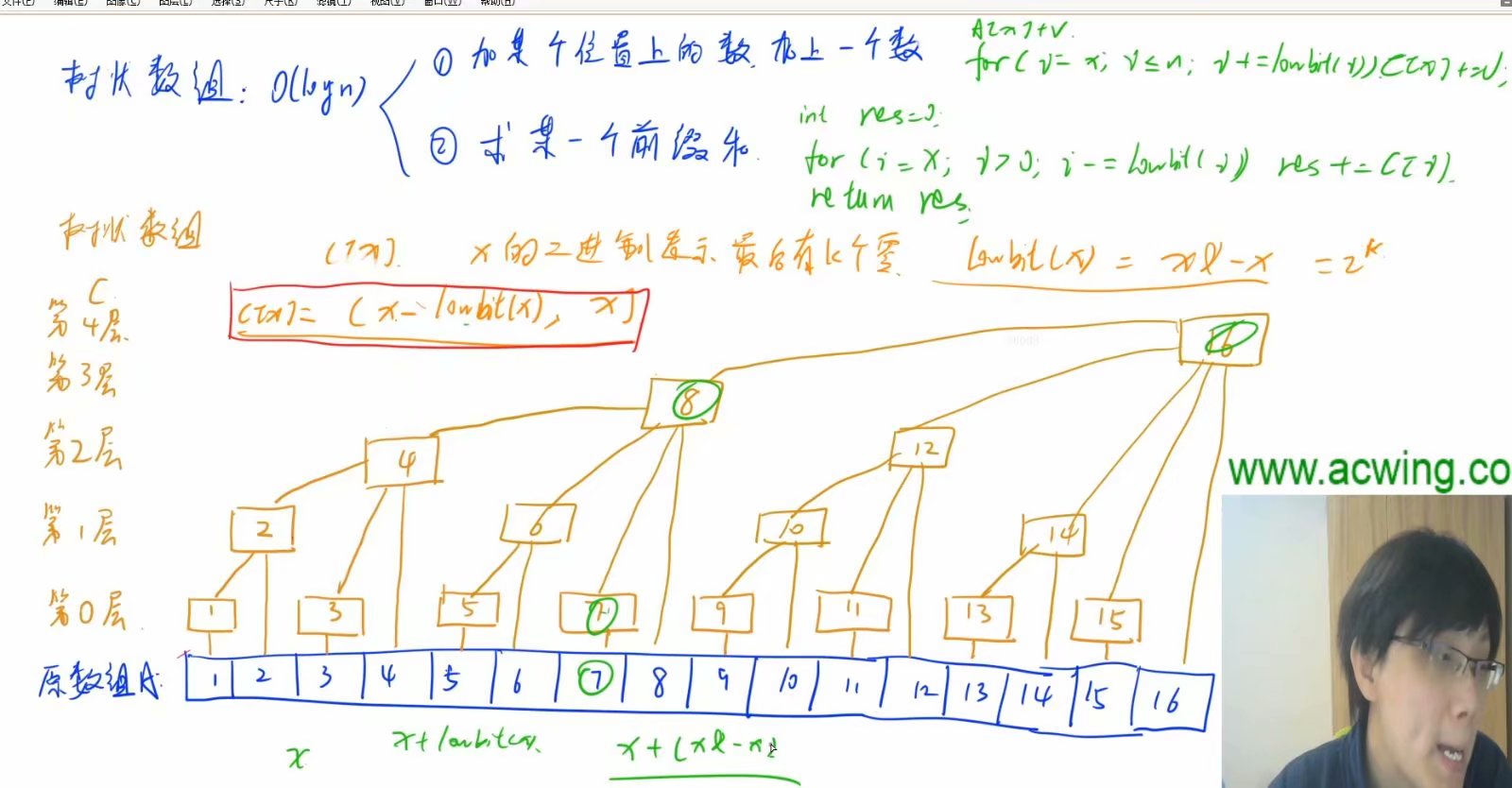
//在x位置加上v，并将后面相关联的位置也加上v，更新C[]

void add(int x,int v){
    for(int i=x;i<=n;i+=lowbit(i)){
        tr[i]+=v;
    }
}

//前缀和

int query(int x){
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int n,m,k;
int a[100005];//原数组 
int tr[100005];//树状数组 
int lowbit(int x){
    return x & -x;
}
//在x位置加上v，并将后面相关联的位置也加上v,更新C[]
void add(int x,int v){
    for(int i=x;i<=n;i+=lowbit(i)){
        tr[i]+=v;
    }
}
//前缀和 
int query(int x){
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}
int main(int argc, char** argv) {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
//搭建树状数组tr[],在刚开始数组默认是全部0,a[]刚开始是0，变成a[i],相当于原数组下标为i的位置上的数加上a[i]
        add(i,a[i]);
    } 
    int x,y;
    while(m--){
        scanf("%d%d%d",&k,&x,&y);
        if(k==1){
            add(x,y);
        }  
        if(k==0){
            printf("%d\n",query(y)-query(x-1));
        }
    }
    return 0;
}

附加y总讲课笔记：

_

_

线段树

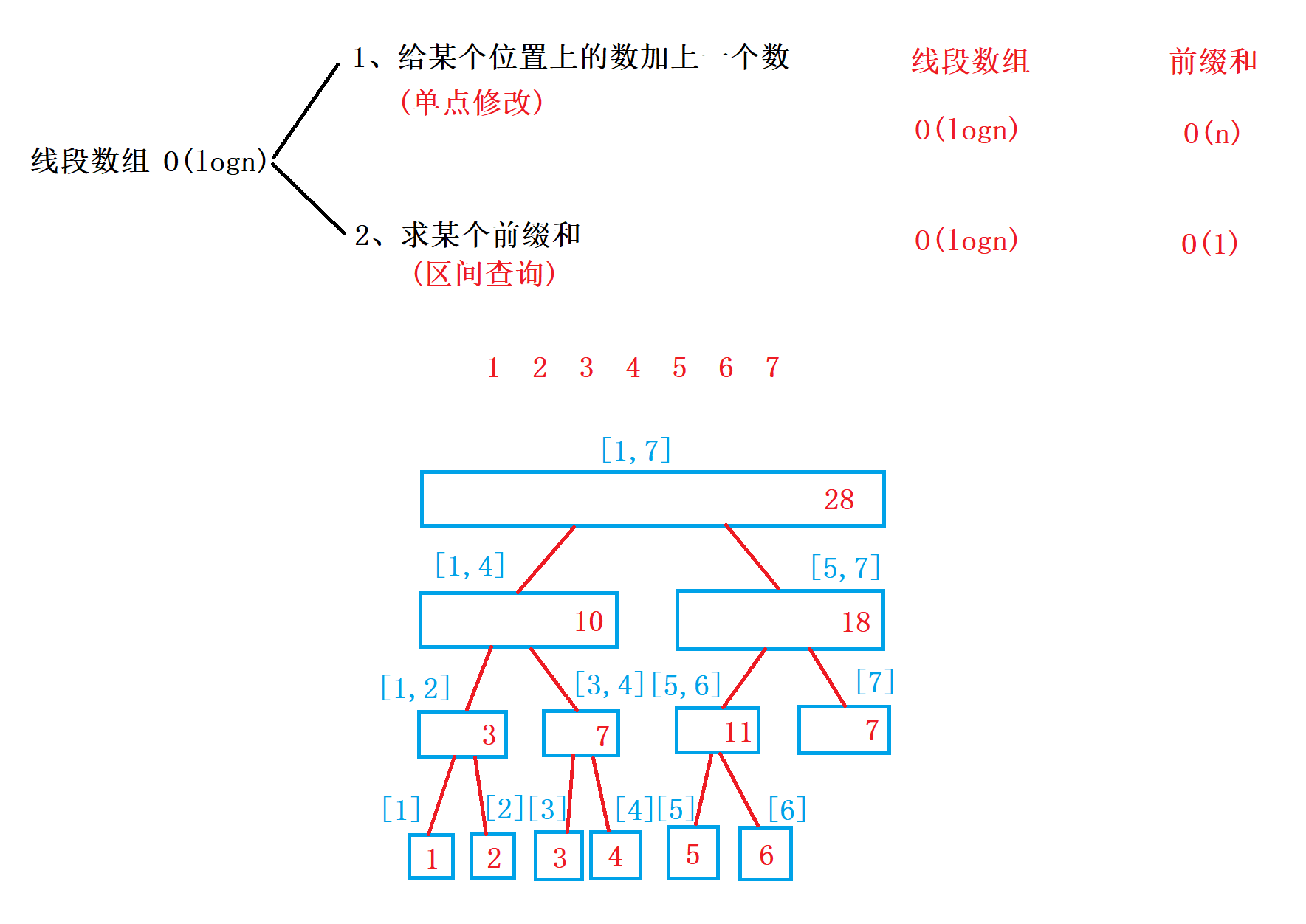
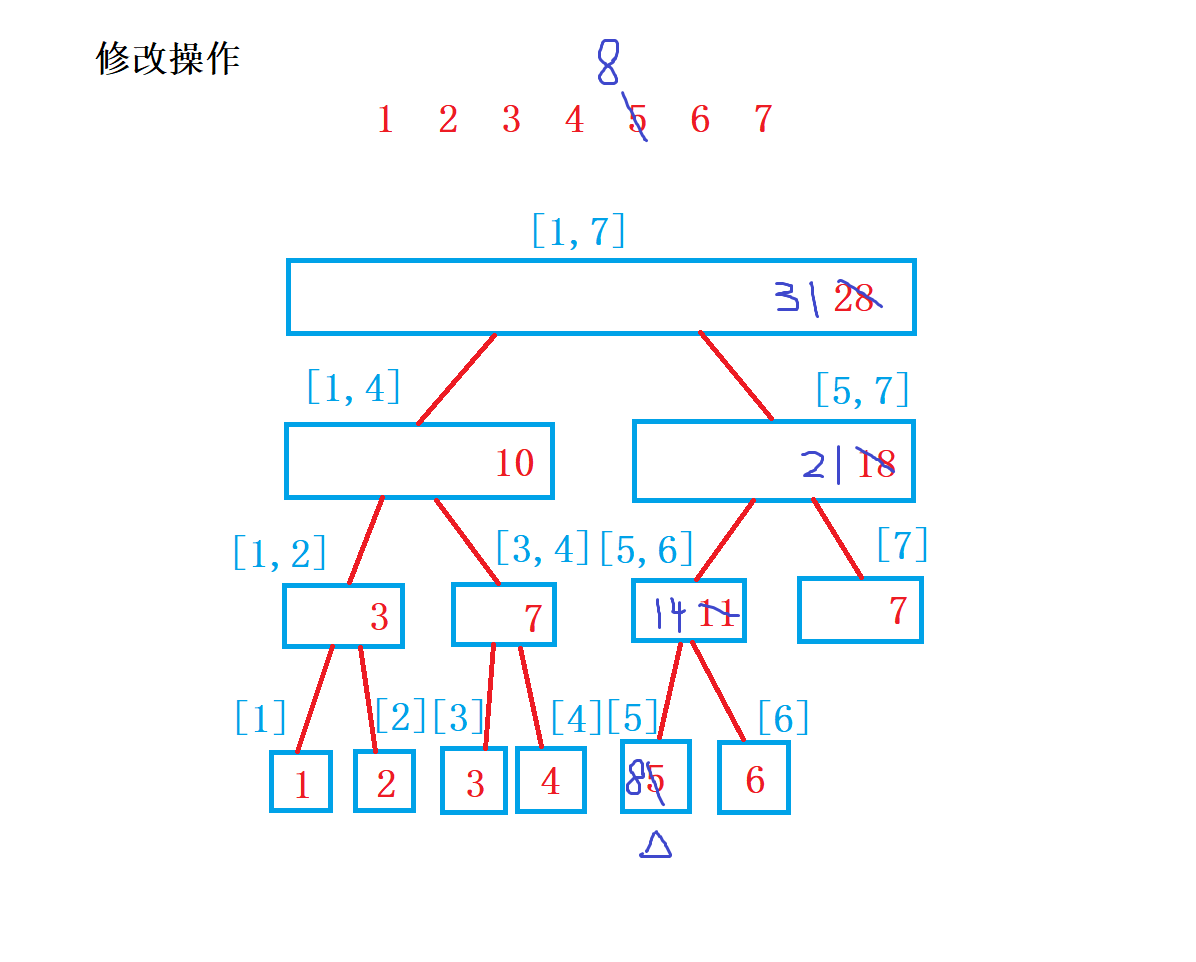
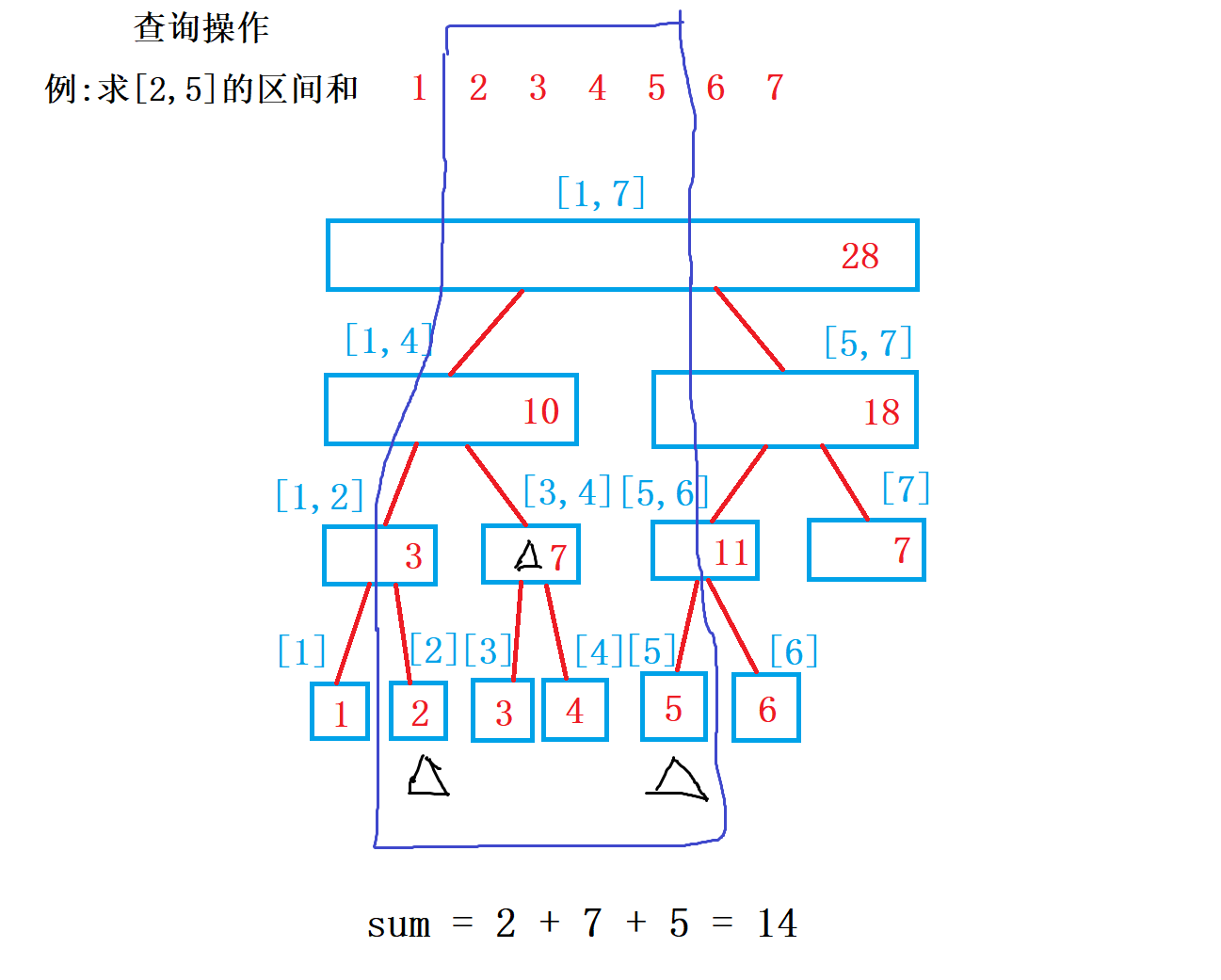
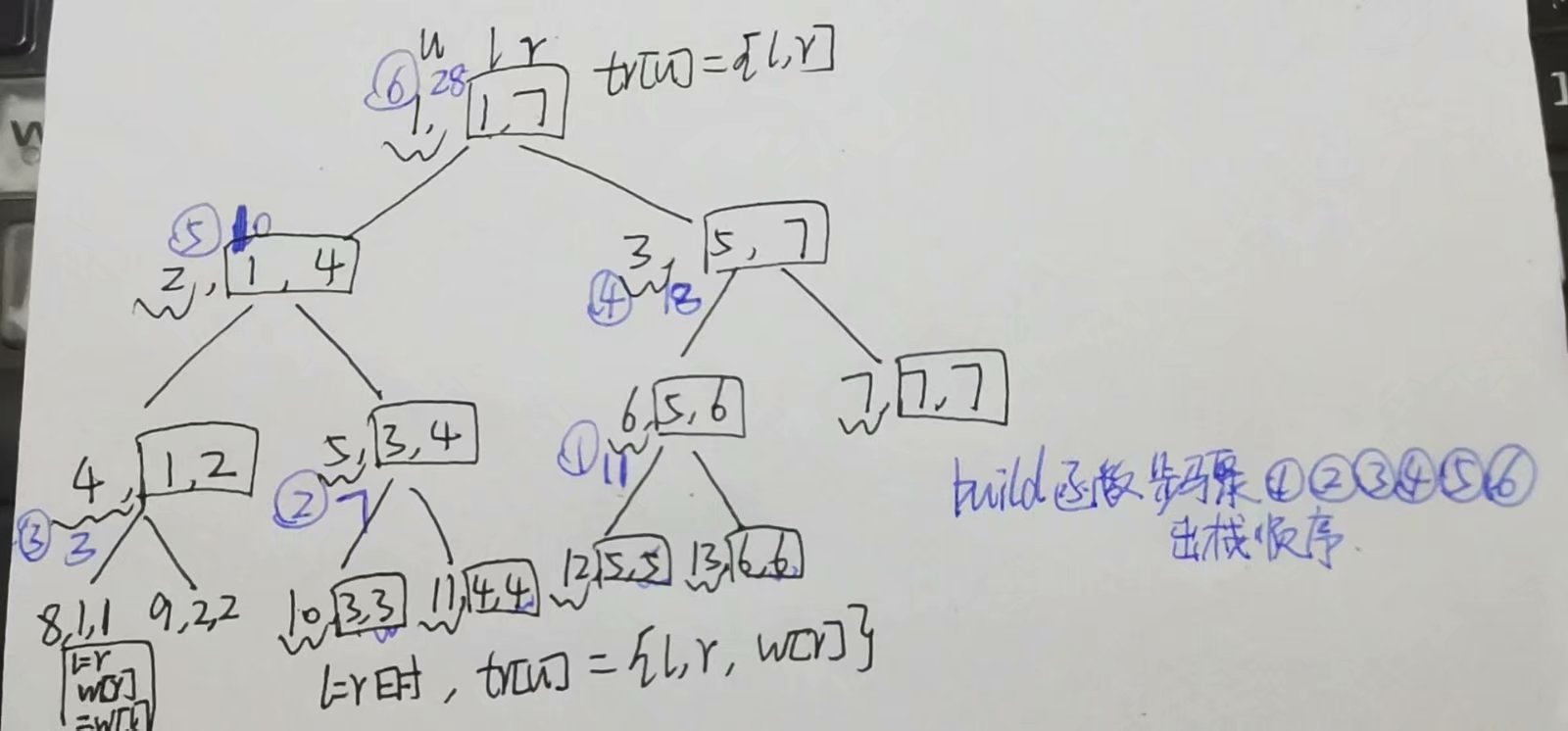
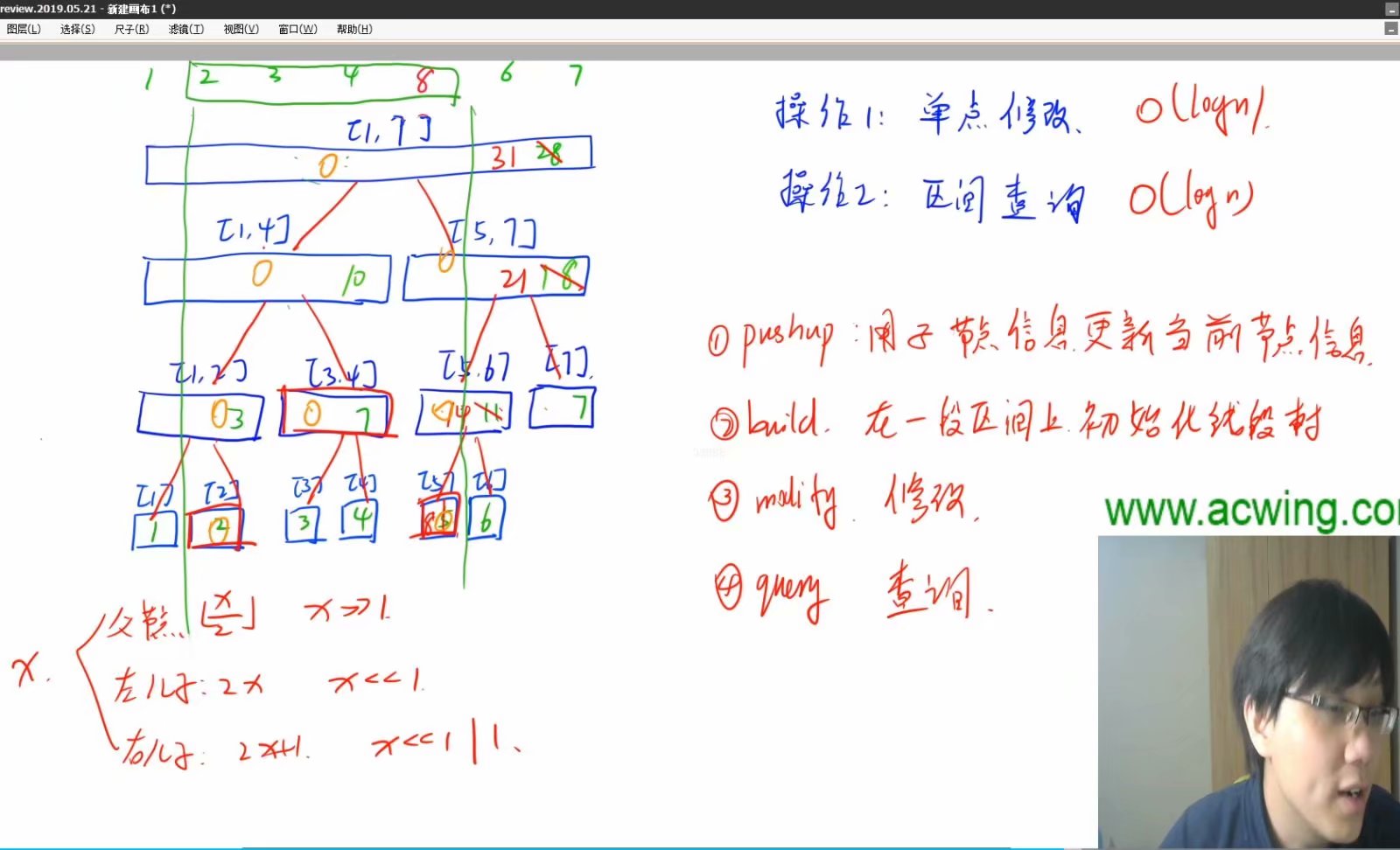
线段树牢记四个公式：
//用子节点信息来更新当前结点信息

void pushup(int u){
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

//在[l,r]一段区间上来初始化线段树，u是根，l是左边界，r是右边界

void build(int u,int l,int r){
    if(l==r) tr[u]={l,r,w[r]};
    else{
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid);build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

//查询操作，查询某段区间的和，前缀和，u是根，l是左边界，r是右边界

int querry(int u,int l,int r){
    if(l<=tr[u].l&&r>=tr[u].r) return tr[u].sum;
    int sum=0;
    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) sum=querry(u<<1,l,r);
    if(r>mid) sum+=querry(u<<1|1,l,r);
    return sum;
}

//修改操作，修改u结点，让x位置上的数加上v

void modify(int u,int x,int v){
    if(tr[u].l==tr[u].r) tr[u].sum+=v;
    else{
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else{
        modify(u<<1|1,x,v);
        }
        pushup(u);
    } 
}

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
using namespace std;
int w[100005];
int n,m;
struct node{
    int l,r;
    int sum;
}tr[400020];
//用子节点信息来更新当前结点信息 
void pushup(int u){
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
//在[l,r]一段区间上来初始化线段树，u是根，l是左边界，r是右边界 
void build(int u,int l,int r){
    if(l==r) tr[u]={l,r,w[r]};
    else{
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid);build(u<<1|1,mid+1,r);
        pushup(u);
    }
}
//查询操作，查询某段区间的和，前缀和，u是根，l是左边界，r是右边界 
int querry(int u,int l,int r){
    if(l<=tr[u].l&&r>=tr[u].r) return tr[u].sum;
    int sum=0;
    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) sum=querry(u<<1,l,r);
    if(r>mid) sum+=querry(u<<1|1,l,r);
    return sum;
}
//修改操作，修改u结点，让x位置上的数加上v 
void modify(int u,int x,int v){
    if(tr[u].l==tr[u].r) tr[u].sum+=v;
    else{
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else{
        modify(u<<1|1,x,v);
        }
        pushup(u);
    } 
}
int main(int argc, char** argv) {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
    scanf("%d",&w[i]);
    }
build(1,1,n);
int k,x,y;
while(m--){
    scanf("%d%d%d",&k,&x,&y);
    if(k==0){
    printf("%d\n",querry(1,x,y));
    }
    else{
    modify(1,x,y);
    }
}
    return 0;
}