$\color{green}{<–画图不易，点下这里赞一下吧}$

朴素迪杰斯特拉算法点这里

优化朴素迪杰斯特拉算法

看一下朴素算法的时间复杂度：

for(i:1 ~ n)//n次
{
    t <- 没有确定最短路径的节点中距离源点最近的点;//每次遍一遍历dist数组，n次的复杂度是O(n^2)
    state[t] = 1;
    更新 dist;//每次遍历一个节点的出边，n次遍历了所有节点的边，复杂度为O(e)
}

算法的主要耗时的步骤是从dist 数组中选出：没有确定最短路径的节点中距离源点最近的点 t。只是找个最小值而已，没有必要每次遍历一遍dist数组。

在一组数中每次能很快的找到最小值，很容易想到使用小根堆。可以使用库中的小根堆（推荐）或者自己编写。

代码：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件

using namespace std;

typedef pair<int, int> PII;//堆里存储距离和节点编号

const int N = 1e6 + 10;

int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接矩阵存储图
int dist[N];//存储距离
bool st[N];//存储状态

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        int ver = t.second, distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (st[ver]) continue;//如果距离已经确定，则跳过该点
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

//参考yxc

使用小根堆后，找到 t 的耗时从 O(n^2) 将为了 O(1)。每次更新 dist 后，需要向堆中插入更新的信息。所以更新dist的时间复杂度有 O(e) 变为了 O(e*logn)。总时间复杂度有 O(n^2) 变为了 O(n + e*longn)。适用于稀疏图。

总结

迪杰斯特拉算法适用于求正权有向图中，源点到其余各个节点的最短路径。注意：图中可以有环，但不能有负权边。

例如：如下图就不能使用迪杰斯特拉算法求节点 1 到其余各个节点的最短距离。
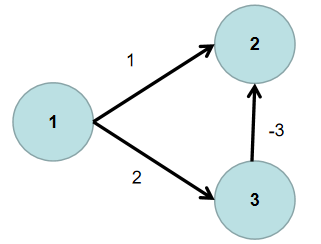{:weith=150 height=150}

求个点赞~~