$\color{green}{<–画图不易，点下这里赞一下吧}$

prim 算法干的事情是：给定一个无向图，在图中选择若干条边把图的所有节点连起来。要求边长之和最小。在图论中，叫做求最小生成树。

prim 算法采用的是一种贪心的策略。

每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

我们将图中各个节点用数字 1 ~ n 编号。

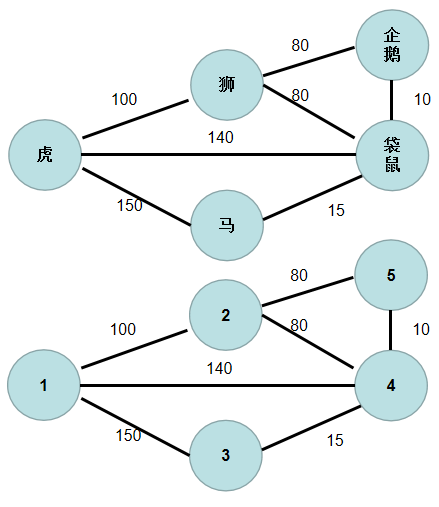
要将所有景点连通起来，并且边长之和最小，步骤如下：

1. 用一个 state 数组表示节点是否已经连通。state[i] 为真，表示已经连通，state[i] 为假，表示还没有连通。初始时，state 各个元素为假。即所有点还没有连通。
   用一个 dist 数组保存各个点到连通部分的最短距离，dist[i] 表示 i 节点到连通部分的最短距离。初始时，dist 数组的各个元素为无穷大。
   用一个 pre 数组保存节点的是和谁连通的。pre[i] = k 表示节点 i 和节点 k 之间需要有一条边。初始时，pre 的各个元素置为 -1。
   

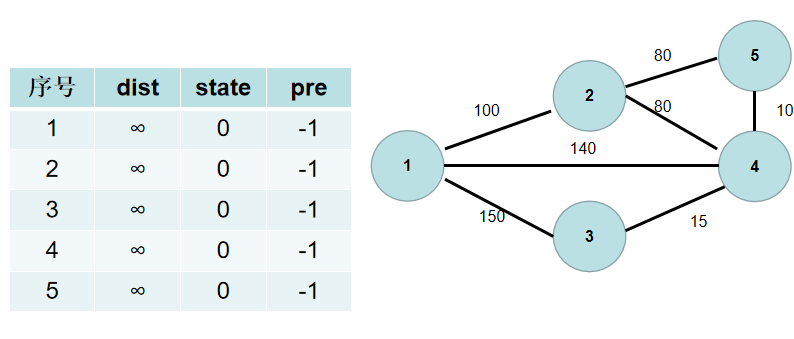
2. 从 1 号节点开始扩充连通的部分，所以 1 号节点与连通部分的最短距离为 0，即disti[1] 置为 0。
   

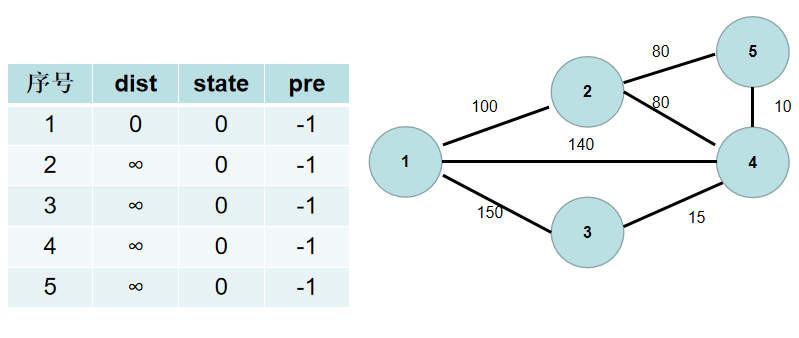
3. 遍历 dist 数组，找到一个还没有连通起来，但是距离连通部分最近的点，假设该节点的编号是 i。i节点就是下一个应该加入连通部分的节点，stata[i] 置为 1。
   用青色点表示还没有连通起来的点，红色点表示连通起来的点。
   这里青色点中距离最小的是 dist[1]，因此 state[1] 置为 1。
   

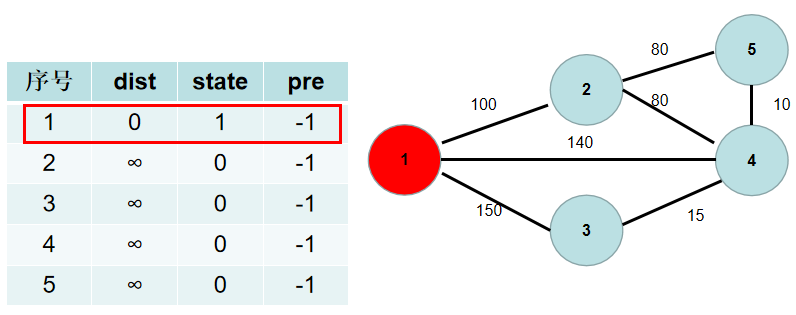
4. 遍历所有与 i 相连但没有加入到连通部分的点 j，如果 j 距离连通部分的距离大于 i j 之间的距离，即 dist[j] > w[i][j]（w[i][j] 为 i j 节点之间的距离），则更新 dist[j] 为 w[i][j]。这时候表示，j 到连通部分的最短方式是和 i 相连，因此，更新pre[j] = i。
   与节点 1 相连的有 2， 3， 4 号节点。1->2 的距离为 100，小于 dist[2]，dist[2] 更新为 100，pre[2] 更新为1。1->4 的距离为 140，小于 dist[4]，dist[4] 更新为 140，pre[2] 更新为1。1->3 的距离为 150，小于 dist[3]，dist[3] 更新为 150，pre[3] 更新为1。
   

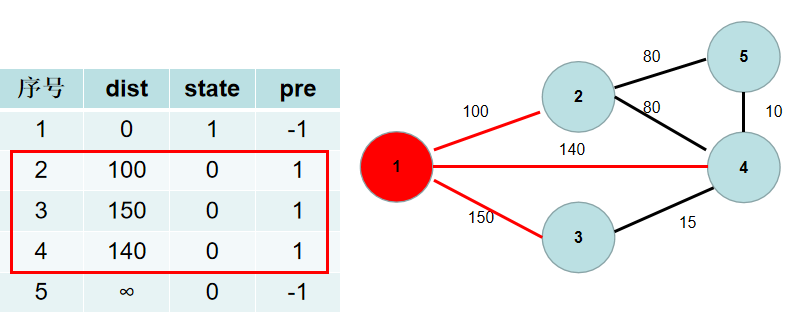
5. 重复 3 4步骤，直到所有节点的状态都被置为 1.
   这里青色点中距离最小的是 dist[2]，因此 state[2] 置为 1。
   
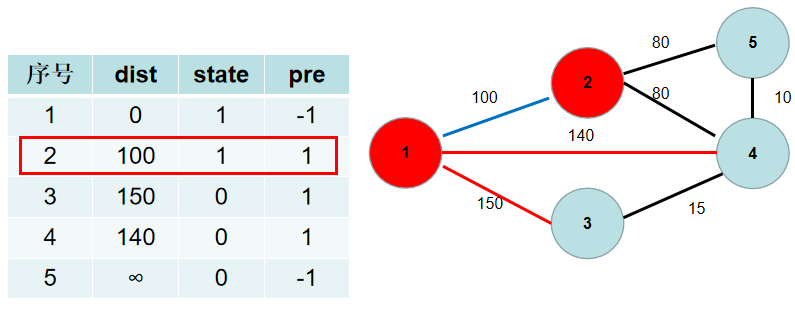
   与节点 2 相连的有 5， 4号节点。2->5 的距离为 80，小于 dist[5]，dist[5] 更新为 80，pre[5] 更新为 2。2->4 的距离为 80，小于 dist[4]，dist[4] 更新为 80，pre[4] 更新为2。
   
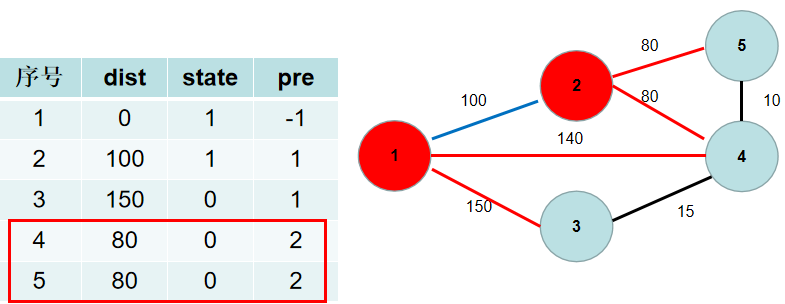
   选dist[4]，更新dist[3]，dist[5]，pre[3]，pre[5]。
   
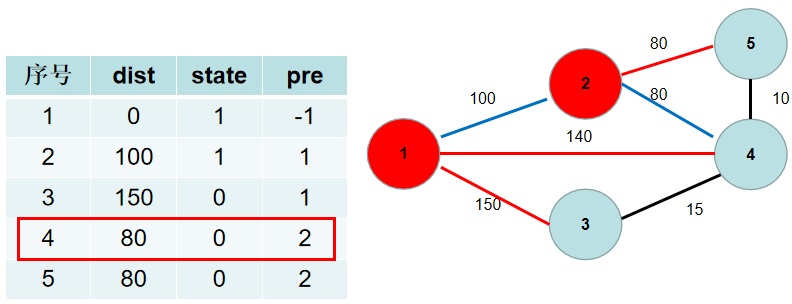
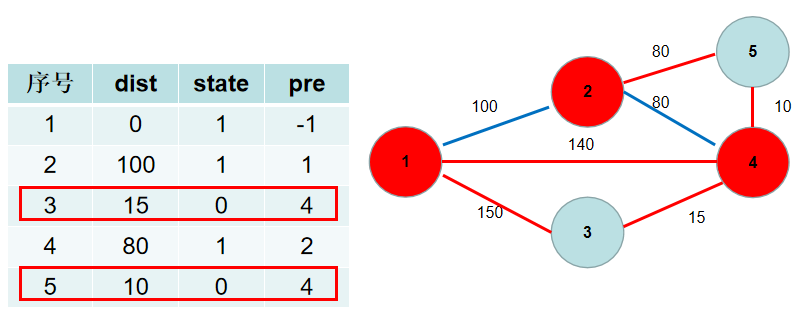
   选dist[5]，没有可更新的。
   
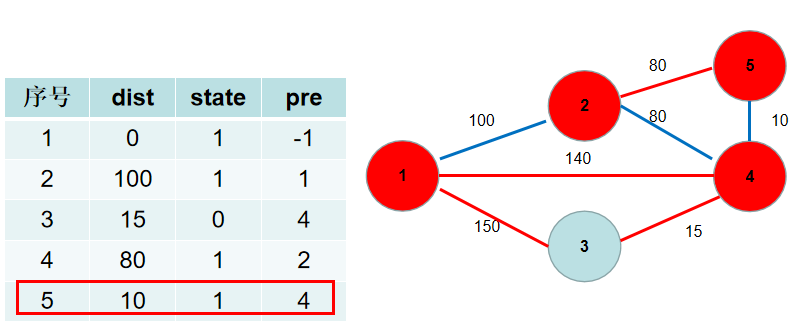
   选dist[3]，没有可更新的。
   

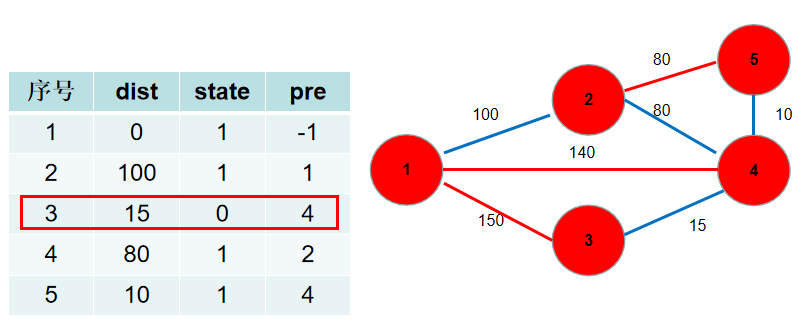
6. 此时 dist 数组中保存了各个节点需要修的路长，加起来就是。pre 数组中保存了需要选择的边。
   

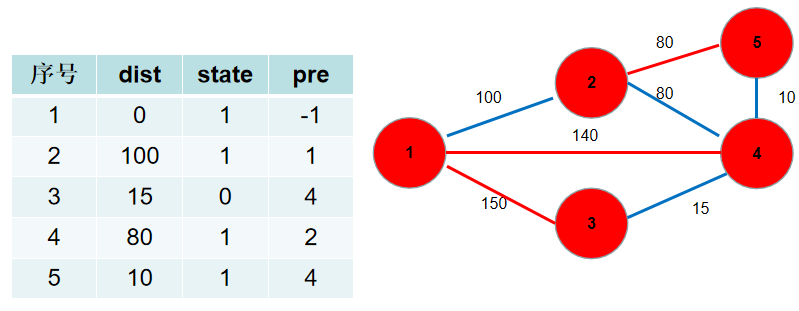
伪代码

int dist[n],state[n],pre[n];
dist[1] = 0;
for(i : 1 ~ n)
{
    t <- 没有连通起来，但是距离连通部分最近的点;
    state[t] = 1;
    更新 dist 和 pre;
}

代码

//2022.6.1 更新

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510;
int g[N][N];//存储图
int dt[N];//存储各个节点到生成树的距离
int st[N];//节点是否被加入到生成树中
int pre[N];//节点的前去节点
int n, m;//n 个节点，m 条边

void prim()
{
    memset(dt,0x3f, sizeof(dt));//初始化距离数组为一个很大的数（10亿左右）
    int res= 0;
    dt[1] = 0;//从 1 号节点开始生成 
    for(int i = 0; i < n; i++)//每次循环选出一个点加入到生成树
    {
        int t = -1;
        for(int j = 1; j <= n; j++)//每个节点一次判断
        {
            if(!st[j] && (t == -1 || dt[j] < dt[t]))//如果没有在树中，且到树的距离最短，则选择该点
                t = j;
        }

        //2022.6.1 发现测试用例加强后，需要判断孤立点了
        //如果孤立点，直返输出不能，然后退出
        if(dt[t] == 0x3f3f3f3f) {
            cout << "impossible";
            return;
        }


        st[t] = 1;// 选择该点
        res += dt[t];
        for(int i = 1; i <= n; i++)//更新生成树外的点到生成树的距离
        {
            if(dt[i] > g[t][i] && !st[i])//从 t 到节点 i 的距离小于原来距离，则更新。
            {
                dt[i] = g[t][i];//更新距离
                pre[i] = t;//从 t 到 i 的距离更短，i 的前驱变为 t.
            }
        }
    }

    cout << res;

}

void getPath()//输出各个边
{
    for(int i = n; i > 1; i--)//n 个节点，所以有 n-1 条边。

    {
        cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号，pre[i] 是 i 节点的前驱节点。他们构成一条边。
    }
}

int main()
{
    memset(g, 0x3f, sizeof(g));//各个点之间的距离初始化成很大的数
    cin >> n >> m;//输入节点数和边数
    while(m --)
    {
        int a, b, w;
        cin >> a >> b >> w;//输出边的两个顶点和权重
        g[a][b] = g[b][a] = min(g[a][b],w);//存储权重
    }

    prim();//求最下生成树
    //getPath();//输出路径
    return 0;
}

优化

上面代码的时间复杂度为 O(n^2)。

与Dijkstra类似，Prim算法也可以用堆优化，优先队列代替堆，优化的Prim算法时间复杂度O(mlogn)。适用于稀疏图，但是稀疏图的时候求最小生成树，Kruskal 算法更加实用。

画图不易，求个点赞~~