题目描述
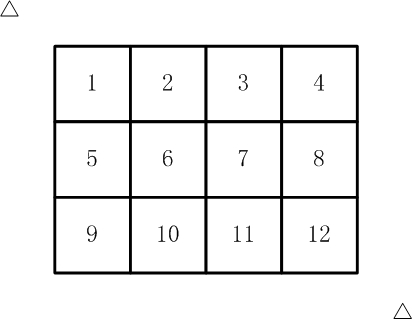
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
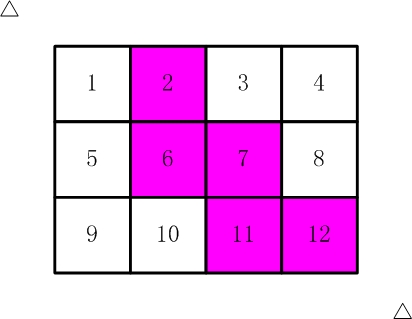
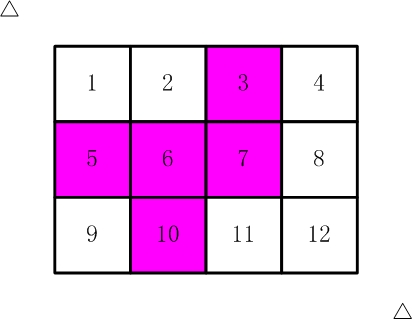
图1图2
请你计算,一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路:直接搜索是不大可能的,我们可以把它转变成全排列问题。因为一共12张,需要5张,我们可以创建一个数组,存放5个1和7个0,然后对其进行全排列(这里值得注意的是普通的全排列对重复的数字会产生重复的全排列,简单起见,我们使用c++里面STL中的next_permutation()),然后将其转化成二维数组,然后用dfs搜索看看有几个连通块,只有一个连通块就是一个可行的方案。
样例
116
C++ 代码
blablabla
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
int w[5][5];
int a[] = {0,0,0,0,0,0,0,1,1,1,1,1}; //随便找出五个方块,然后对这五个方块的摆放位置进行全排列
int match[5][5]; //记忆化数组记录为1的方块是是否被遍历过了
int dx[] = {0,1,0,-1},dy[] = {1,0,-1,0};
void dfs(int x,int y){ //遍历连通块
match[x][y] = 0; //遍历过的方块变为0
for(int i = 0;i < 4;++i){
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 3 && nx >= 0 && ny < 4 && ny >= 0 && match[nx][ny]){
dfs(nx,ny);
}
}
}
bool check(){ //判断当前a数组当中所有是1的方块是否都是在用一个连接块当中
int cnt = 0;
for(int i = 0;i < 3;++i){ //将当前的a数组拉成二维用match记录下来
for(int j = 0;j < 4;++j){
match[i][j] = a[i * 4 + j]; //把a数组拉成二维数组成为match数组
}
}
for(int i = 0;i < 3;++i){
for(int j = 0;j < 4;++j){
if(match[i][j] == 1){
dfs(i,j); //将(i,j)所在的连通块全部遍历一遍
cnt++; //当前代码块 + 1
}
}
}
return cnt == 1;
}
int main(){
int res = 0;
do{
if(check()) res++;
}while(next_permutation(a,a + 12));
printf("%d",res);
}

