思想

倍增:

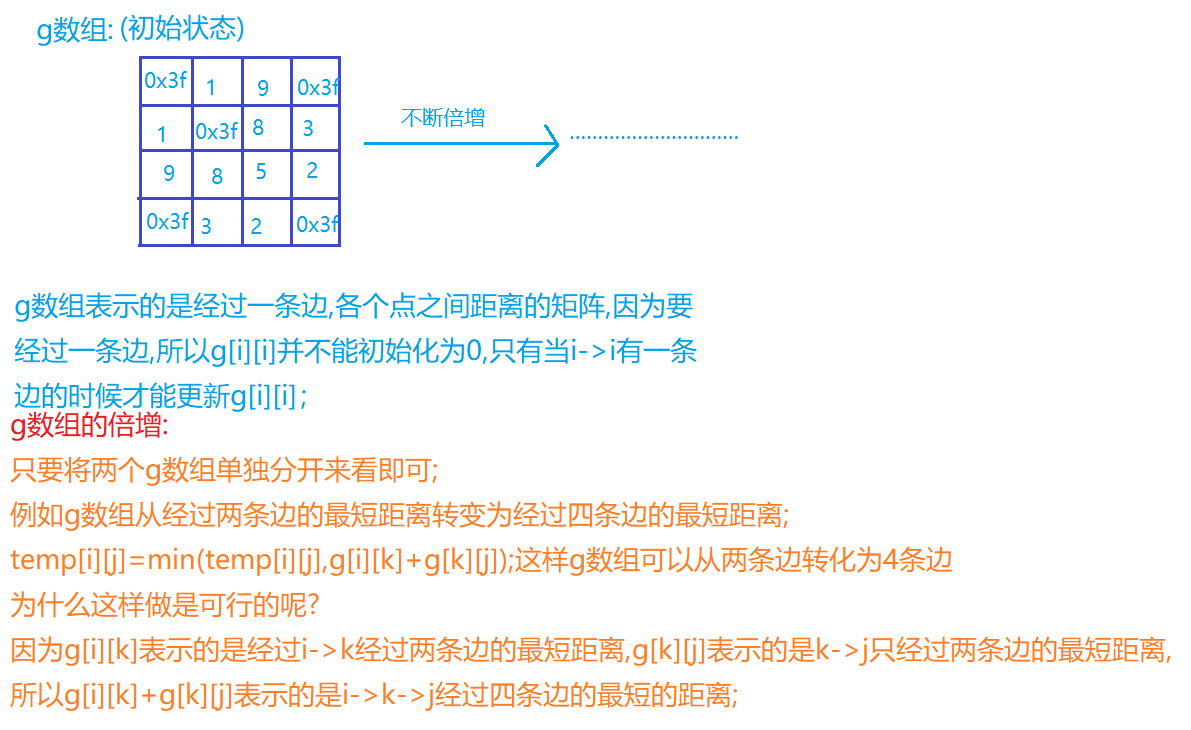
这种方式在数学上称之为矩阵乘法;

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>

using namespace std;

const int N=1010;

int K,n,m,S,E;

int g[N][N];//开始为只经过一条边的数组
int res[N][N];//答案数组


void floyd(int a[][N],int b[][N],int c[][N])
{
    static int temp[N][N];//temp数组作为b数组和c组数相乘的结果

    memset(temp,0x3f,sizeof temp);

    for(int k=1;k<=n;k++)
     for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
       temp[i][j]=min(temp[i][j],b[i][k]+c[k][j]);

    memcpy(a,temp,sizeof temp);   //复制得到结果
}

void qmi()//快速幂套floyd
{
    memset(res,0x3f,sizeof res);
    for(int i=1;i<=n;i++) res[i][i]=0;

    while(K)
    {
        if(K&1) floyd(res,res,g);//更新答案数组,即res=res*g
        floyd(g,g,g);//将g数组倍增,即g=g*g
        K>>=1;
    }
}

int main()
{
    cin>>K>>m>>S>>E;
    map<int,int> id;
    memset(g,0x3f,sizeof g);
    //因为g数组必须走过一条边,所以g[i][i]不初始化为0,除非i->i之间有边

    id[S]=++n,id[E]=++n;
    S=id[S],E=id[E];

    //离散化过程,因为题目中给的编号并不是从1开始而是随机的;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>c>>a>>b;
        if(!id.count(a)) id[a]=++n;
        if(!id.count(b)) id[b]=++n;
        a=id[a],b=id[b];
        g[a][b]=g[b][a]=min(g[a][b],c);
    }

    qmi();

    printf("%d",res[S][E]);//输出答案

    return 0;
}

如果有问题,欢迎在下方指出