题目描述

给定一个数组，包含 $n$ 个正整数。你从起点(0,0)开始，x[0]表示往北走的距离，x[1]表示往西走的距离，x[2]表示往南走的距离，[x3]表示往东走的距离，依次类推。换句话说，你一直在按顺时针方向转圈。

请编写一个函数，判断走过的路径是否相交。
只能使用额外 $O(1)$ 的空间。

样例1

给定 x = [2, 1, 1, 2],
?????
?   ?
???????>
    ?

返回 true (路径相交)

样例2

给定 x = [1, 2, 3, 4],
????????
?      ?
?
?
?????????????>

返回 false (路径不相交)

样例3

给定 x = [1, 1, 1, 1],
?????
?   ?
?????>

返回 true (路径相交)

算法

(分情况讨论) $O(n)$

我们分类讨论相交的情况有哪些。一共有三种：

1. 连续的四条边相交：
   
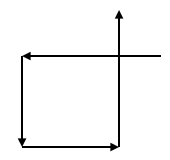
2. 连续的五条边相交：
   
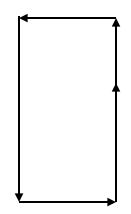
3. 连续的六条边相交：
   

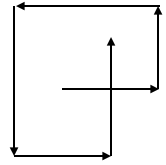
然后遍历整个数组，判断这三种情况即可。

时间复杂度分析：整个数组仅被遍历一次，所以时间复杂度是 $O(n)$。

C++ 代码

class Solution {
public:
    bool isSelfCrossing(vector<int>& x) {
        int n = x.size();
        if (n <= 3) return false;
        for (int i = 3; i < n; i ++ )
        {
            if (x[i] >= x[i - 2] && x[i - 1] <= x[i - 3]) return true;
            if (i >= 4 && x[i - 1] == x[i - 3] && x[i] + x[i - 4] >= x[i - 2]) return true;
            if (i >= 5 && x[i - 2] >= x[i - 4] && x[i] + x[i - 4] >= x[i - 2] && x[i - 1] + x[i - 5] >= x[i - 3]  && x[i - 1] <= x[i - 3]) return true;
        }
        return false;
    }
};