优化方式1(无需证明)

优化方式2(证明)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=70;
int w[N],sum,length,n;
bool st[N];
bool dfs(int u,int part,int start)//第u组,part第u组的已有长度,start表示第u组的枚举位置;
{
if(u*length==sum) return true;//如果总长度到达了,返回true
if(part==length) return dfs(u+1,0,0);//true要一直持续不断的返回,false同理
for(int i=start;i<=n;i++)
{
if(st[i]) continue;
if(w[i]+part>length) continue;
st[i]=true;//标记已经使用
if(dfs(u,w[i]+part,i+1)) return true;//因为前i个棍子都在第u组枚举了,所以直接从第i+1根棍子开始枚举
st[i]=false;//返回上层分支时要恢复现场(枚举该组不选择第i根根子的方案)
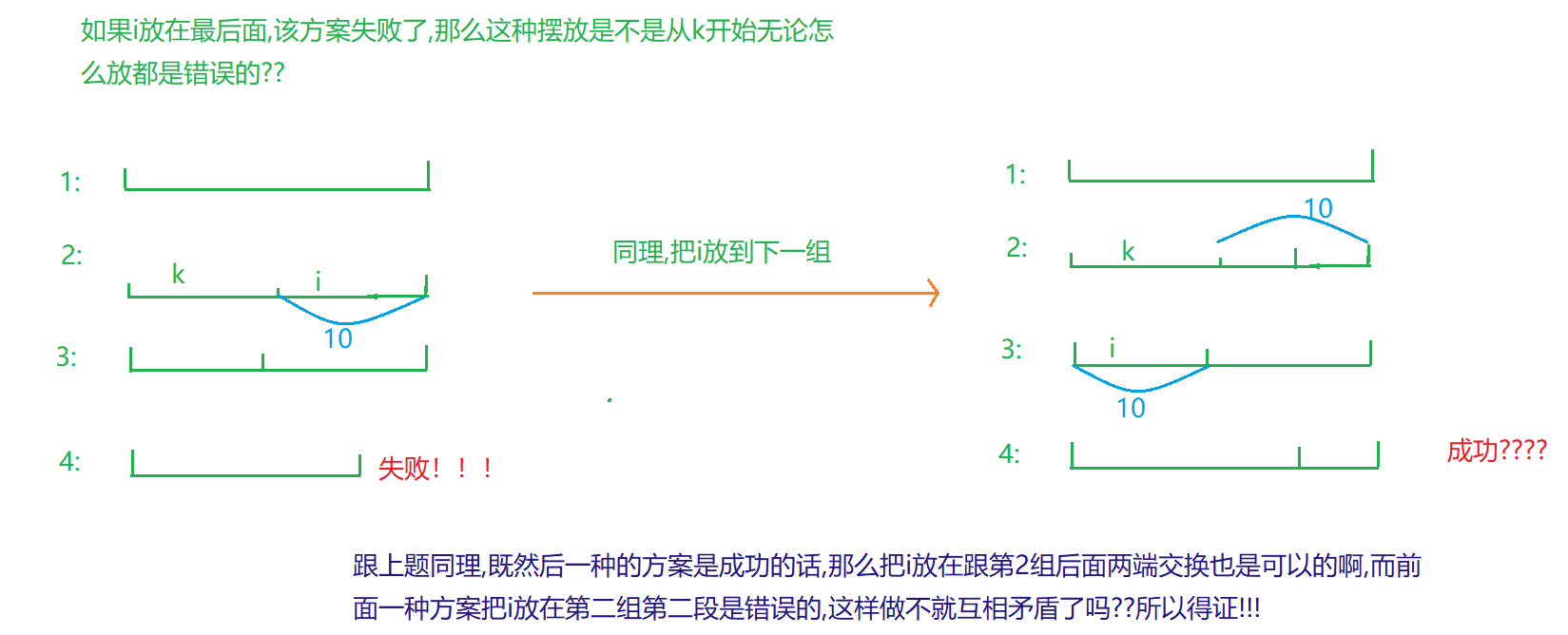
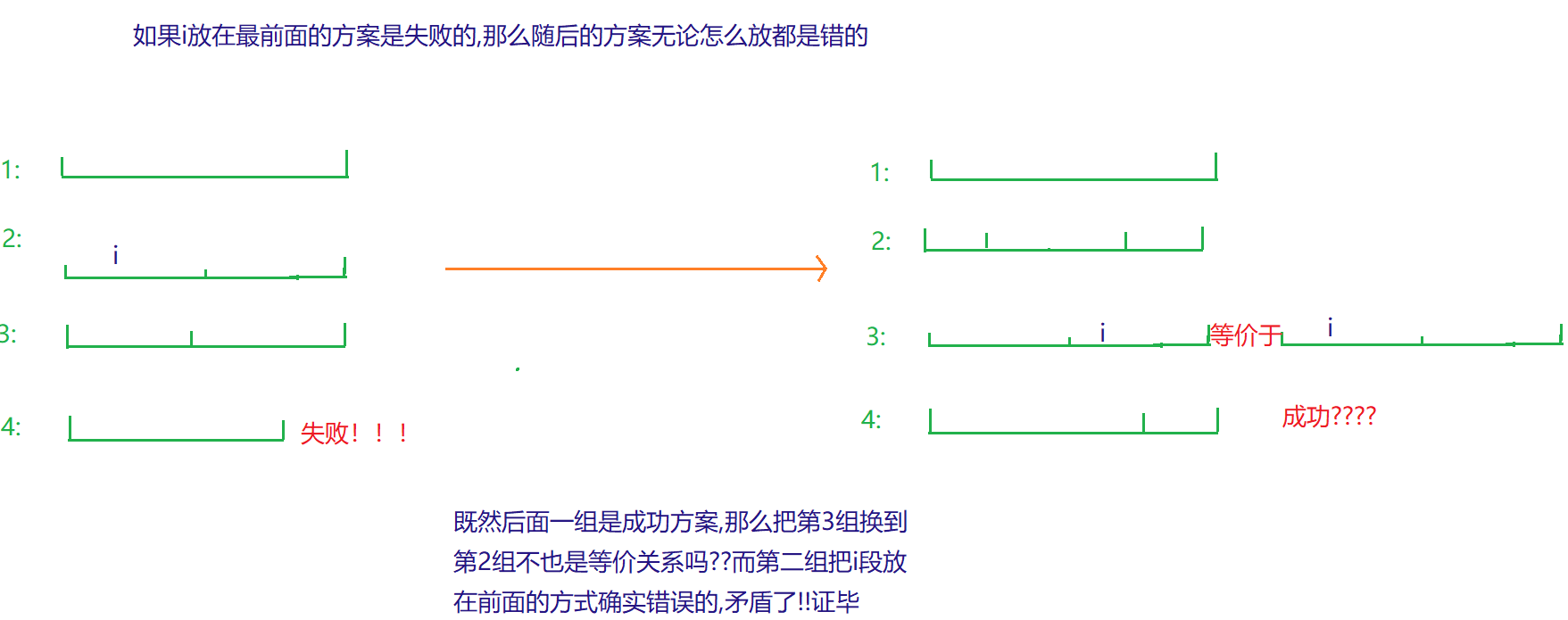
if(!part||w[i]+part==length) return false;//如果第一根失败了或者最后一根失败了,就一定失败
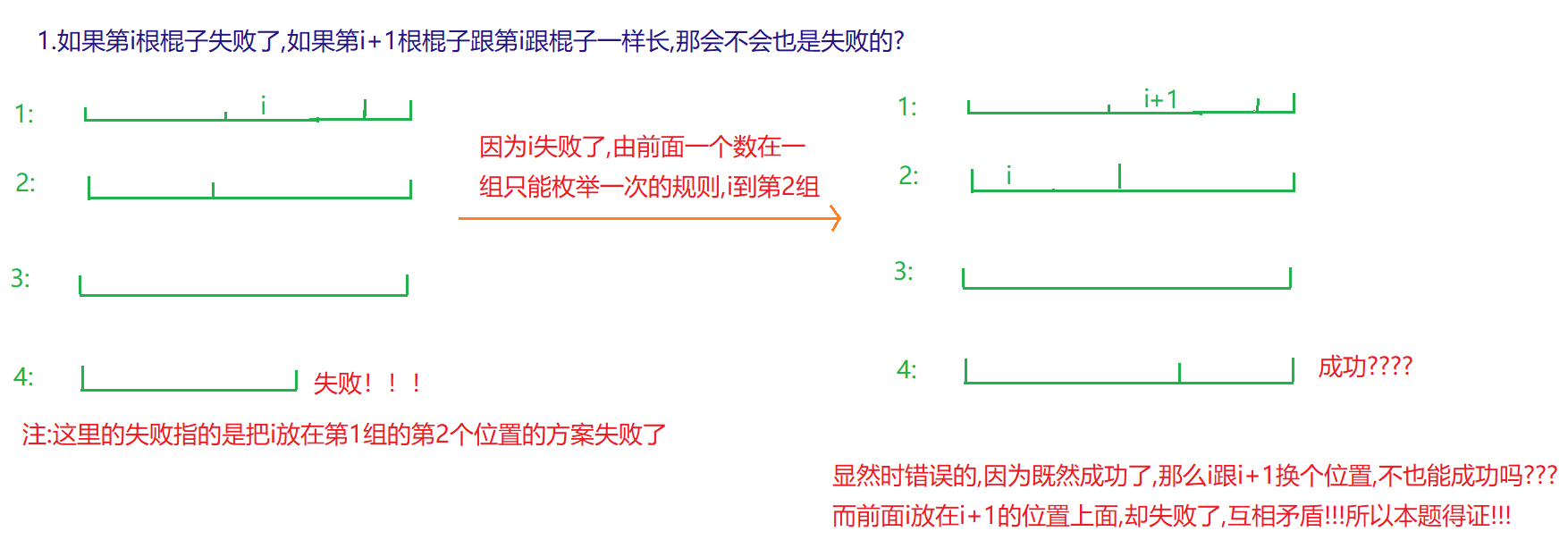
int j=i;//如果i失败了,那么长度跟i一样的棍子也一定失败
while(j<=n&&w[j]==w[i]) j++;
i=j-1;
}
return false;//枚举完了还没有成功,就返回失败
}
int main()
{
while(cin>>n,n)
{
//初始化
memset(st,0,sizeof st);
sum=0,length=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&w[i]);
sum+=w[i];//总和
}
//倒着排序,以减少分支
sort(w+1,w+n+1);
reverse(w+1,w+n+1);
while(1)//枚举length的长度
{
if(sum%length==0&&dfs(0,0,0))
{
printf("%d\n",length);
break;
}
length++;
}
}
}


感觉大家在理解剪枝的时候要抓住我们的棍子是递减遍历这个重要特性去理解,不然只会越来越混乱,下面给出我自己的理解:
剪枝1:所有数都按照从大到小的顺序排列
剪枝2:若第i个棍子失败了,之后与第i个棍子长度相同的也会失败
剪枝3:若第i个棍子作为第一个失败了,那么总体是失败的,因为我们是按照从大到小的顺序排列的,如果在组成第j个木棒失败,那么在组成第j+1个木棒的时候,第i个棍子也是会被当成第一个的,也一定会失败。以此类推,后面所有的木棒把第i个棍子当作第一个都会失败,当要组成最后一个木棒时,第i个棍子必须是第一个,因为我们规定了长度递减,然而这种情况是失败的,所以总体失败。
剪枝4:若第i个棍子作为最后一个失败了,那么总体是失败的,反证法:如果不用第i个棍子,而是比第i个棍子小的几个棍子的组合,之后的木棒包含第i个棍子,交换这个棍子组合和第i个棍子,当前木棒仍然成立且仍然满足棍子长度递减的关系,在另一个木棒中经过交换也满足递减的关系,发现了可行方案,所以矛盾了。
在剪枝3:没说会在j+1出现 伪证
不是伪证
这里是怎么确定如果第一根失败了或者最后一根失败了呢?
同问,什么叫失败了
没有成功就是失败了😂
看起来好像是废话文学, 但如果上面需要恢复现场的地方成功了就会直接return了, 是不会运行到这一步的
dfs的第一行是总的大成功(所有组都凑成length了), 而第二行是阶段性胜利(这一组凑成length了), 只有深度遍历到最底层得到总的大成功了, 才会return true,失败有各种各样的, 可能是前x组都阶段胜利了, 最后一组没凑成; 也可能是前x-1组都胜利了, 倒数第二组被剪枝了
所以失败就是用这根棍子没有达到最后大成功, 没有成功就是失败了
谢谢你
w[i]+part==length 为啥用它来表示是 最后一根?
明白了吗同学,能教一下吗?最后这个剪枝好难啊。。
明白了吗同学,我也很迷
模模糊糊,半个月前做的了,现在也忘了hh
因为加上它之后长度为length,所以他就是第u层的最后一根木棍。
第u层最后一根木棍拼好之后,会继续拼下面的层数的木棒。
如果下面的层数都能拼好,也就是所以木棍不重不漏的拼成了木棒,第u层会返回给u-1层true,而u-1层的return dfs(u+1,0,0);会继续将true返回给u-2层,就这样一直返回下去直到主函数里。
一旦下面出现了一层凑不出木棒的(上一层能凑出)就会返回false给上一层。返回给上一层之后会先传递到上一层最后一根木棍,而这根木棍满足part+w[i]==length,但是由于前面判断语句if(dfs(u,w[i]+part,i+1))不成立,会继续往下走,遇到if(!part||w[i]+part==length) return false;后返回false
题解里的true和false在递归函数之间的传递非常耐人寻味
懂了哥
讲得好
st[i] = true; if (dfs(i + 1, cnt, val + a[i])) return true; 1 st[i] = false; if (!val || val + a[i] == len) return false; 2重要的是这几步,剪枝34难以理解。
这里有一个前提,就是一找到解整个递归立马就会return true结束掉。
这里递归1,就是如果该木棍放到当前的情况下,并且找得到最终结果,直接return true,整个递归结束了。
如果还需要复原现场,那么就是该木棍按当前方式放(虽然放的进大棍儿里),但是最终搜不到合法解,那就可以pass掉。
剪枝3
至于第一根和最后一根
如果放置该小根儿到第一根之后,递归到最后总是找不到解,那么可以直接剪枝,该小棍儿不能放到第一个。
中间的小根儿可以调整
最后一根,并不是完全意义上的最后一根,而是放上这一小根后刚好等于len的小根儿,此前val + a[i] > len 的已经被剪掉,而 val + a[i] < len 的还需要dfs递归到下一层去找解。那么当这最后一根必然不可能找到解,因为上面递归1 不是true啊
不理解为什么最后一根不行就全部都不行了,不能是后面两组中各抽出一根木棒组成这个长度的,然后后面两组再重新组合下,不存在这种巧合吗?
最后一根不行,是表示找不到一组合法的题目要求的解,而不是表示放在当前大木中不合法。
假如一根小木放在当前大木中最后一个不行,那么可以判断它放在任何一根大木中都不行,不存在题目要求的可以把所有小木放在若干个大木中正好放满。
上面判断的证明:反证法:假如有一根小木放在当前大木x的最后一根不行,但是放在其他大木y的任意位置行,则大木y中该小木可以通过平移使得该小木置于最后一个位置,这样就存在方案使得该小木放在大木最后一个位置可行,与假设相悖,得证。
可是考虑最后一个的时候,是考虑顺序的吧,怎么平移的时候又不考虑顺序了呢
这里的start是可以去掉的,因为只要长度够了便下一组,不够则继续找。想不懂的小伙伴也可以删掉没有影响的。
dfs(int u,int part,int start)中start表示的是第u组的枚举位置,但是在一开始枚举的时候木棒中是没有木棍的,那么为什么start一开始为0呢?
这是因为前面木棒枚举的时候可能没有组成目标长度的木棒,这个时候再从头枚举可能会将前面比较长的木棒与后面比较短的木棒匹配从而组合成目标长度的木棒
你这个下标怎么是从1开始的。。。调用的时候又是
dfs(0, 0, 0)?dfs(0, 0, 1)也AC.
牛
#include[HTML_REMOVED]
#include[HTML_REMOVED]
#include[HTML_REMOVED]
using namespace std;
const int N = 70;
int n, sum, len, cnt;
int a[N];
int st[N];
bool dfs(int stick, int cur, int last)
{
if(stick == cnt) return true;
if(cur == len) dfs(stick + 1, 0, 1); //剪枝3 若拼失败,跳过所有等长木棒 int fail = 0; //剪枝2 for(int i = last; i <= n; i ++) { if(!st[i] && cur + a[i] <= len && a[i] != fail) { st[i] = 1; if(dfs(stick, cur + a[i], i + 1)) return true; //注意这句话的位置 fail = a[i]; st[i] = 0; //剪枝4,5 空木棒的等效性 贪心 if(cur == 0 || cur + a[i] == len) return false; } } return false;}
int main()
{
ios::sync_with_stdio(false);
while(cin >> n && n) { sum = 0; int val = 0; for(int i = 1; i <= n; i ++) { cin >> a[i]; sum += a[i]; val = max(val, a[i]); } //剪枝1 优先选长度最长的木棒 sort(a + 1, a + n + 1); reverse(a + 1, a + n + 1); //求最小长度 for(len = val; len <= sum; len ++) { if(sum % len) continue; cnt = sum / len; memset(st, 0, sizeof st); if(dfs(1, 0, 1)) break; } cout << len << endl; } return 0;}
有大佬可以帮我看看哪里错了吗,一直改不出来,第一个样例也过不了
要理解剪枝3和4,重点在于理解它是从哪里剪掉的。对于3,设失败的第一个小木棒为x,剪掉说明上一层的这里 if(part==length) return dfs(u+1,0,0);返回false.然后就会退回到上一根木棒的最后一个,由于4,再退回到上一个,也就是清除了上一根木棒的最后两个小木棍,然后从这里重新枚举其他可能。但是没有这个剪枝的话,就会从x所在木棍清除x后开始枚举下一根小木棒。如果是这样的话,那么假设成功,x也一定会在某个木棍的第一个,(因为如果有比x更长的木棒在x前面的情况应该更先考虑),那么就导致了矛盾。
大佬 可以用void dfs吗
如果固定区间后,此状态一定不行,那么说明上一状态出了问题,返回上一状态。
而在中间非固定区间,所以可以当前状态可能行
为什么我T了a
#pragma GCC optimize(2) #pragma GCC optimize(3) #include <iostream> #include <cstring> #include <algorithm> #include <cstdio> #include <cmath> using namespace std; const int N = 74; int n, a[N]; int sum, len; bool st[N]; bool cmp(int p, int q) { return p < q; } bool dfs(int x, int now, int la) { if (x * len == sum) { return true; } if (now == len) { return dfs(x + 1, 0, 0); } for (int i = la; i <= n; i ++ ) { if (st[i]) { continue; } if (a[i] + now > len) { continue; } st[i] = true; if (dfs(x, now + a[i], i + 1)) { return true; } st[i] = false; if (!now || now + a[i] == len) { return false; } int j = i; while (j <= n && a[j] == a[i]) { j ++ ; } i = j - 1; } return false; } int main() { while (scanf("%d", &n) && n) { memset(st, 0, sizeof st); sum = 0; for (int i = 1; i <= n; i ++ ) { scanf("%d", &a[i]); sum += a[i]; } sort(a + 1, a + 1 + n, cmp); for (len = 1; len <= sum; len ++ ) { if (sum % len == 0 && dfs(0, 0, 0)) { printf("%d\n", len); break; } } } return 0; }这里都能发现秃秃大佬(我用cmp也T
md,数据太毒了,改
reverse就过了话说我也很sb,把cmp里的大于打成小于了你这不是升序排序吗
吼吼吼吼吼吼吼吼吼吼吼吼吼吼吼吼
暂时看懂了部分
插个眼提醒回来自己回来学习大佬的证明插眼()
看懂了感谢
我感觉你这里的图解好像有点问题,在方案失败的情况下,应该有一根木棒比当前枚举的 lenth 要长,一根木棒比lenth 更短,否则就不能满足枚举长度是总长约数的条件
我觉得说得有道理
第一根失败的情况是在if(dfs(u,w[i]+part,i+1))条件不成立的情况下执行的嘛,或者说这些第一根失败和某一根失败相同长度的木棒都失败的剪枝都是在if条件失败的情况下执行的嘛
可以认为if(dfs(u,w[i]+part,i+1))条件不成立,代表剩下所有木棒都无法与当前这跟木棒组合成指定length,所以后面怎么都解决不掉这根木棒,所以return false;
但是中间某一根失败可以换跟比他短点的解决正在拼的这组,然后后面新的一组再用这跟中间没用上的