最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

有 $n$ 个 任务 排成一个 序列，顺序不得改变，其中第 $i$ 个 任务 的 耗时 为 $t_i$， 费用系数 为 $c_i$

现需要把该 $n$ 个 任务 分成 若干批 进行加工处理

每批次的 段头，需要 额外消耗 $S$ 的时间启动机器。每一个任务的 完成时间 是所在 批次 的 结束时间。

完成一个任务的 费用 为：从 $0$ 时刻 到该任务 所在批次结束 的时间 $t$ 乘以 该任务 费用系数 $c$

分析

关于本题朴素版的DP分析，可以看该篇博客：AcWing300. 任务安排1【线性DP+费用提前计算思想】

贴出朴素版的 状态转移方程：

$$ f_i = \min\bigg(f_j + S \times (sc_n - sc_j) + st_i \times (sc_i - sc_j)\bigg) $$

提出式子中 含有单独 $i$ 的常量：$f_i = st_i\times sc_i + S \times sc_n + \min\bigg(f_j - S \times sc_j - st_i \times sc_j\bigg)$

考察 $min$ 函数内部的 多项式：$f_j - sc_j \times (S + st_i)$

该式子中，有 $i \times j$ 的项，因此不能直接用上一章节中提到的 滑动窗口 来维护一个前缀的 最值

但是 分析的思想 可以继承，我们知道 含 $i$ 的项是一个 常量，故该 多项式 就能够 抽象 成如下形式：

$$ f_j - sc_j \times (S + st_i) = 变量1 - 变量2 \times (常量S + 常量i) $$

注意，这里的 变量1 和 变量2 并不是两个 独立变量 （该 函数 非 多元函数）

变量1 $f_j$ 是与 $j$ 有关的 变量，变量2 $sc_j$ 也是与 $j$ 有关的 变量

因此，不妨令 $\begin{cases} f_j = y(j) \\\\ sc_j = x(j) \\\\ k = S+st_i \end{cases}$，则该函数可以化为：$y(j) - k \cdot x(j)$

为了式子 方便观察，接下来我会把 $y(j)$ 写成 $y$，$x(j)$ 写成 $x$，但是请读者心中明白，这两个 变量，都是关于 $j$ 的 变量（学过 高数 的，直接类比 参数方程 即可）

求 $y - kx ~ (0 \le j \lt i)$ 函数的极值问题，可以直观想到 直线的斜截式方程：$y = kx + b$

对 直线的斜截式方程 进行变形：$b = y - kx$

要求 $y - kx ~ (0 \le j \lt i)$ 函数的极值，就是求一个点 $(x_j, y_j)$ 与当前 $k_i$ 构成的 所有直线 中，y轴截距最小

为了方便各位读者理解，在这贴上一幅图，为大家 几何直观 的展示这一过程：

正如华罗庚先生说过的：数缺形时少直观，形少数时难入微，数形结合百般好

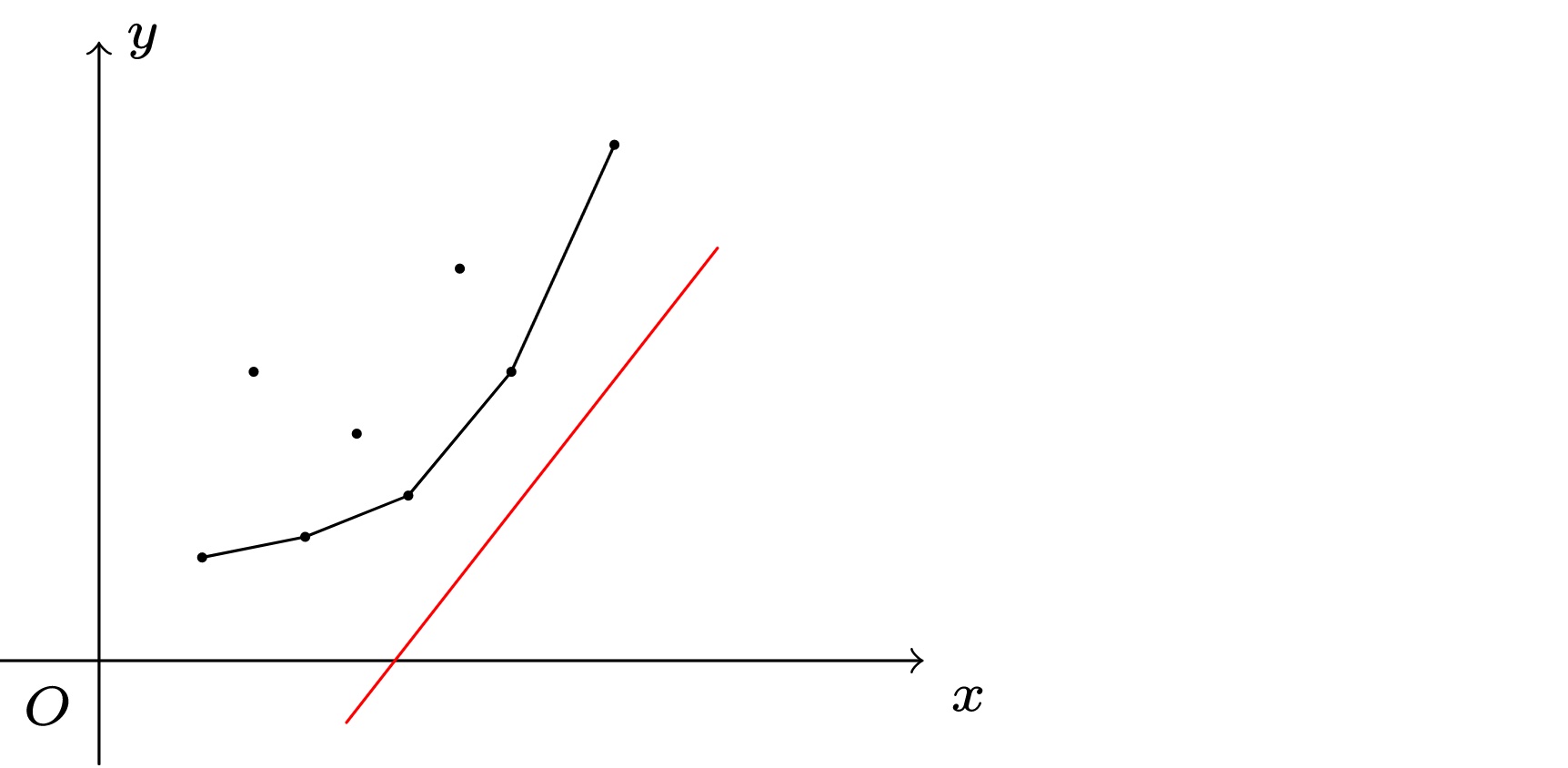
图中，黑色点 为所有 $0 \le j \lt i$ 的点 $(x_j,y_j)$，红色线 为 斜率 是 $k_i$ 的 某一条直线

我们 从下往上（截距从小到大） 去逼近当前 所有的点
则 第一个 出现在直线上的点，就是满足 $b_i = y_j - kx_j$ 的 最小截距 $b_i$，即是当前阶段 DP 的 最佳策略

那么，如何有效的维护点集呢？

这就是一个 线性规划 的问题了：在 点集 中，找到一个 点，绘制 固定斜率 的直线，使得 截距最小

由 线性规划 知识可知：我们只用考虑 点集 中 凸壳 上的点即可

几何直观 上，显然这题要维护的是 下凸壳

因此，对于任意的 $f_i$ 来说，我们只需去寻找 下凸壳 上的 点 构成 直线 的 最小截距 即可

这样 时间复杂度 在 最坏 的情况下，还是 $O(n^2)$（即 所有点 的 $(x,y)$ 单增，全部点 构成一个 下凸壳）

斜率优化了个寂寞？并非如此！我们再看看直线方程中，各参数的性质

由于 $t_i, c_i$ 都是 正整数，故他们的 前缀和 $st_i,sc_i$ 是 单调递增的

对应于 直线方程的参数：$x_j = sc_j$ 是 单调递增 的，$k_i = S + st_i$ 也是 单调递增 的

而 下凸壳 中 相邻两点 构成的直线 斜率 也是 单调递增 的

则 下凸壳 中第一个出现在 直线 上的点，满足：$k_{j-1, j} \le k_i \lt k_{j,j+1}$，此时 直线截距 $b_j$ 最小

大家可以配合下图几何直观理解该处的不等式

而又由于 $k_i$ 单调递增，所以 $j$ 之前 的 点 都不会是 点集 中出现在 直线 上的 第一个点

此时只需 维护点集区间 $[j,i]$ 的 点 即可，直到 $k_{j,j+1} \le k \lt k_{j+1,j+2}$ 时，维护点集区间 变为 $[j+1,i]$

根据上述所说，出现了我们最熟悉的模型-滑动窗口模型。

故我们可以直接利用 单调队列 来维护 下凸壳中的有效点集

并用队头的 两个元素 维护 大于当前斜率 $k_i$ 的最小斜率 $k_{q_{hh}~,~q_{hh+1}}$

这里我把公式展开，方便大家理解：

$$ k_{q_{hh}~,~q_{hh+1}} \gt k_i \Rightarrow \frac{y_{q_{hh+1}}-y_{hh}}{x_{q_{hh+1}}-x_{hh}} \gt k_i \Rightarrow \frac{f_{q_{hh+1}}-f_{hh}}{sc_{q_{hh+1}}-sc_{hh}} \gt S+st_i $$

把点插入 单调队列 前，先要 队列 中 至少有两个点，然后把 满足 $k_{q_{tt-1}~,~q_{tt}} \ge k_{q_{tt}~,~i}$ 的 点 $q_{tt}$ 弹出

即 新加入的点，必须和 原点集 构成 下凸壳，无效点要先删去

这里我把公式展开，方便大家理解：

$$ k_{q_{tt-1}~,~q_{tt}} \lt k_{q_{tt}~,~i} \Rightarrow \frac{y_{q_{tt}}-y_{q_{tt-1}}}{x_{q_{tt}}-x_{q_{tt-1}}} \lt \frac{y_{i}-y_{q_{tt}}}{x_{i}-x_{q_{tt}}} \Rightarrow \frac{f_{q_{tt}}-f_{q_{tt-1}}}{sc_{q_{tt}}-sc_{q_{tt-1}}} \lt \frac{f_{i}-f_{q_{tt}}}{sc_{i}-sc_{q_{tt}}} $$

这样，队列 中 相邻两点 之间构成的直线 斜率单增，也就是我们的 有效下凸壳点集

斜率优化DP模板（来源：Oi-Wiki）

上面密密麻麻零零散散写了一堆分析，最后我们来把 斜率优化 总结成一个 模板，方便大家记忆：

1. 将初始状态入队
2. 每次使用一条和 $i$ 相关的直线 $f_i$ 去切维护的凸包，找到最优决策，更新 $dp_i$
3. 加入状态 $dp_i$。如果一个状态（即凸包上的一个点）在 $dp_i$ 加入后不再是凸包上的点，需要在 $dp_i$ 加入之前剔除

斜率优化往往还要再套一层 二分/CDQ/平衡树优化
不过本题直接用单调队列就好了，上述优化方法的题目会在今后的博客中提到（有生之年）

Code

时间复杂度： $O(n)$

这题非常的好，希望大家不要抄代码，好好推一遍 w

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 3e5 + 10;

int n, S, que[N];
LL st[N], sc[N], f[N];

int main()
{
    scanf("%d%d", &n, &S);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%lld%lld", &st[i], &sc[i]);
        st[i] += st[i - 1], sc[i] += sc[i - 1];
    }

    int hh = 0, tt = 0; que[0] = 0;
    for (int i = 1; i <= n; i ++ )
    {
        while (hh < tt && (f[que[hh + 1]] - f[que[hh]]) <= 
                          (sc[que[hh + 1]] - sc[que[hh]]) * (st[i] + S)) 
            hh ++ ;
        f[i] = f[que[hh]] + S * (sc[n] - sc[que[hh]]) + st[i] * (sc[i] - sc[que[hh]]);
        while (hh < tt && (f[que[tt]] - f[que[tt - 1]]) * (sc[i] - sc[que[tt]]) >=
                          (f[i] - f[que[tt]]) * (sc[que[tt]] - sc[que[tt - 1]]))
            tt -- ;
        que[ ++ tt] = i;
    }
    printf("%lld\n", f[n]);
    return 0;
}