思路分析

1. 首先看题目，可以看出应该在 1 ~ N 个数中， 应该把它们分为三个集合，但是题目给出的信息并不是一个完整的合并集合的信息，即两个数之间的关系并不是直接给出的，而是我们需要进一步判断两个数之间的关系再把它合并到对应的集合中去，故这里如果只有个p[N]数组存储其集合根结点的信息是不够的。
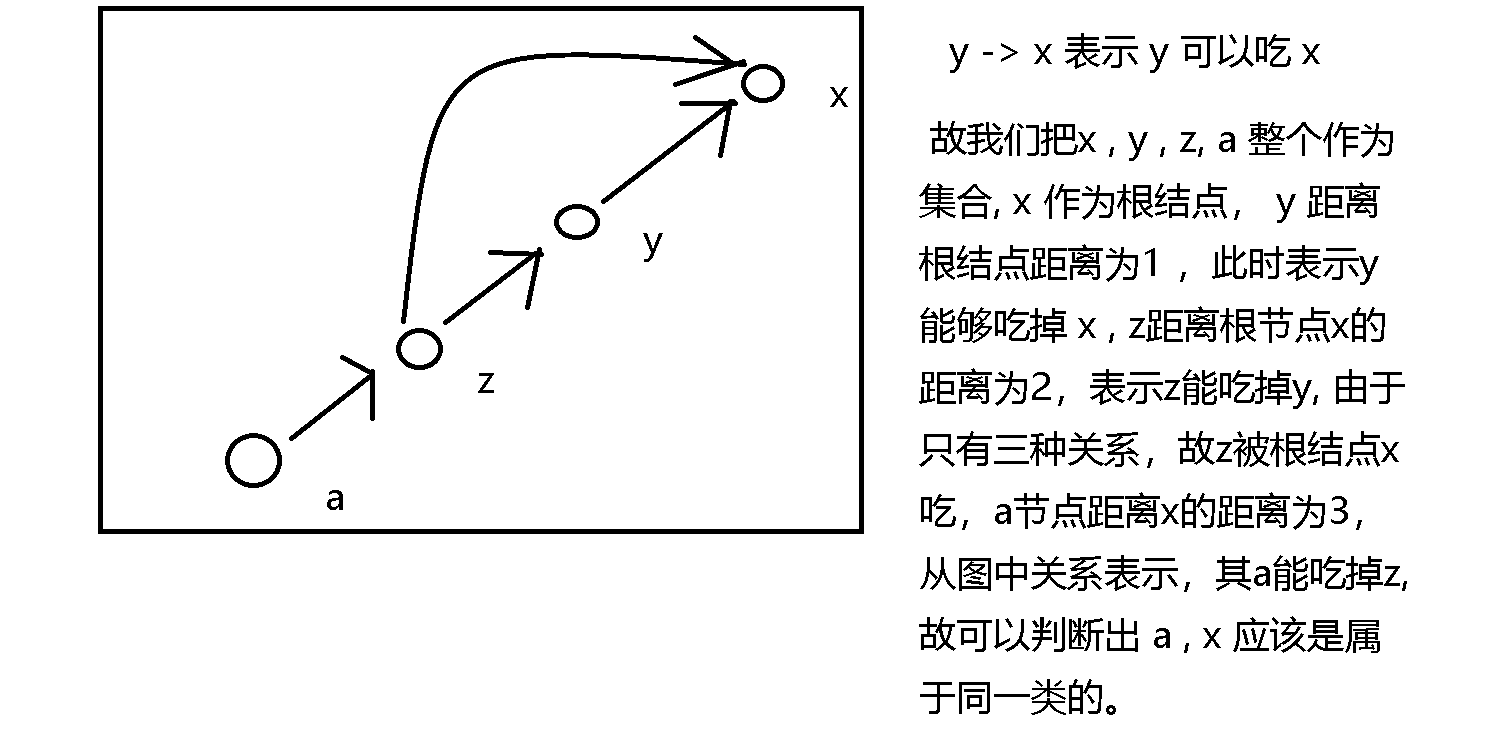
2. 故我们需要存储一些额外的信息来表示两个数字之间的关系， 但是如何表示其二者的关系，这里y总的方法很巧妙的是用一个d[N]数组存储当前元素距离其所在集合根结点的距离， 距离的含义用下面图比较好理解.
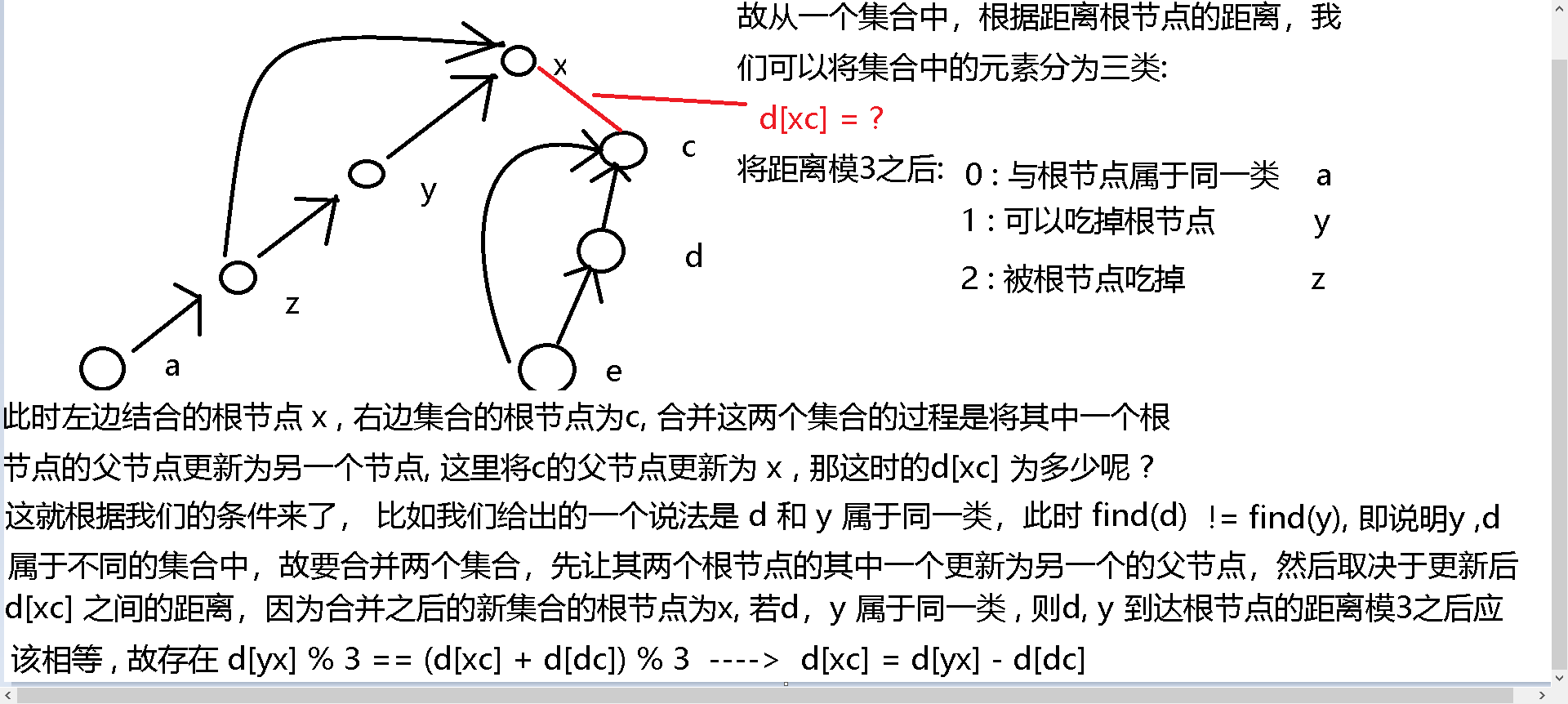
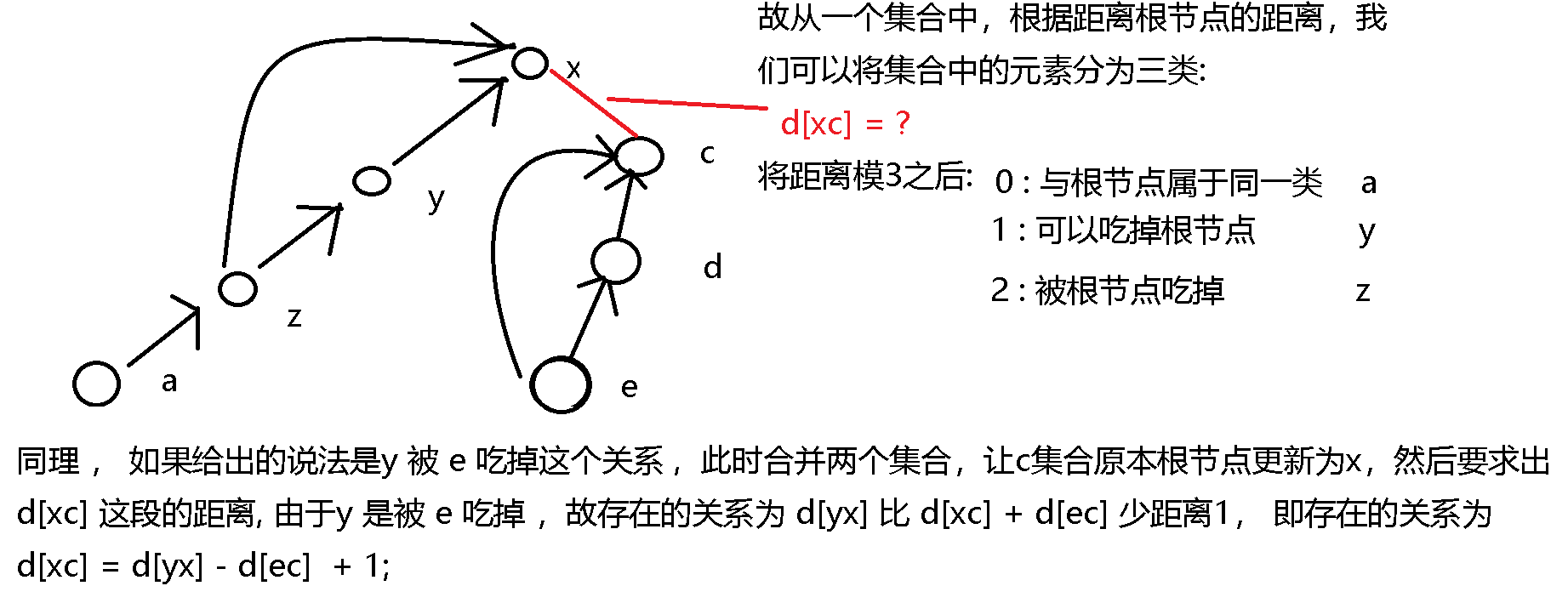
3. 如图所示
   

#include<iostream>
using namespace std;
constexpr int N = 1e+5 + 10;

int n, m, p[N], d[N];

auto find(int x) -> int
{
    if(p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];    // 这里直接路径压缩, 直接通过递归更新为从x 到 所在集合根节点的距离
        p[x] = t;
    }
    return p[x];
}

auto main() -> int
{
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) p[i] = i;
    int res = 0;
    while(m--)
    {
        int op, x, y; cin >> op >> x >> y;
        int px = find(x), py = find(y);
        if(x > n || y > n) ++res;           // 判断为假，给出的x, y 超出n
        else
        {
            if(1 == op)                     // 说法为两个元素属于同一类
            {
            // 先判断是否属于同一集合, 只有位于同一集合才能判断关系,故先判断 px == py, 
            // 若属于同一集合判断与根节点的距离，若属于同一类(d[x] - d[y]) % 3 == 0,
            // 否则不为0，该if条件成立, 说明为假 , ++res;
                if(px == py && (d[x] - d[y]) % 3) ++res;  
                else if(px != py)                // 再次判断若二者属于不同集合，则进行合并操作
                {
                    p[px] = py;             // 合并过程如上面的分析
                    d[px] = d[y] - d[x];
                }
            }
            else 
            {
                if(px == py && (d[x] - d[y] - 1) % 3) ++res;
                else if(px != py)
                {
                    p[px] = py;
                    d[px] = d[y] - d[x] + 1;
                }

            }
        }
    }
    cout << res << endl;
    return 0;
}