题目描述

对于一个具有树特征的无向图，我们可选择任何一个节点作为根。图因此可以成为树，在所有可能的树中，具有最小高度的树被称为最小高度树。给出这样的一个图，写出一个函数找到所有的最小高度树并返回他们的根节点。

一棵树是一个任意两个节点恰好有一条路径连接的无向图。换句话说，任何一个没有简单回路的连通图就是一棵树。

给定 n 个节点和 n-1 条边的一棵树，edges[i] = [a_i, b_i] 表示节点 a_i 和 b_i 之间有一条无向边，你可以任意选择树中的一个节点作为根。当你选择节点 x 作为根时，最终树的高度记为 h。在所有可能的有根树中，拥有最小高度 min(h) 的树叫做 最小高度树 MHT。

返回列表包含 MHT 的所有根节点。你可以以 任意顺序 返回答案。

一棵有根树的 高度 为从根节点到叶子之间最长路径所经过的边数。

样例

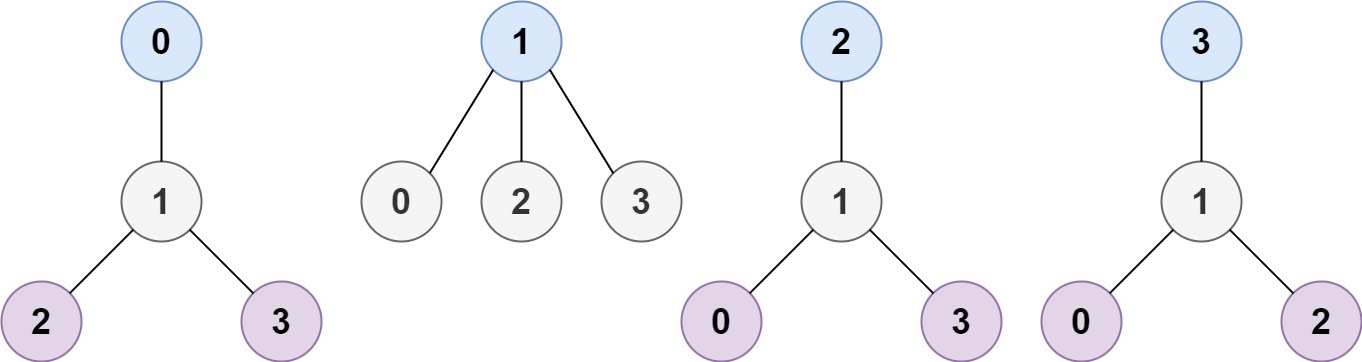
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，仅有一个 MHT，其根节点是 1。

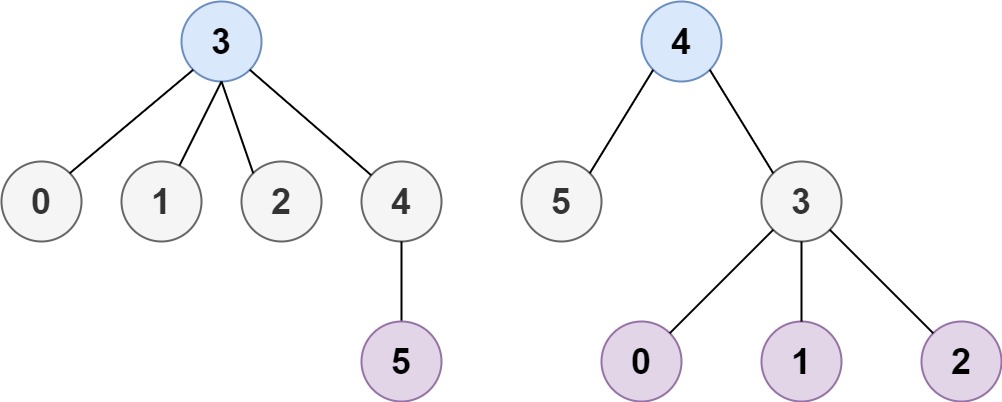
输入：n = 6, edges = Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

输入：n = 1, edges = []
输出：[0]

输入：n = 2, edges = [[0,1]]
输出：[0,1]

限制

• 1 <= n <= 2 * 10^4
• edges.length == n - 1
• 0 <= ai, bi < n
• a_i != b_i
• 所有数对 (a_i, b_i) 都是不同的。
• 给定的输入 保证 是一棵树。

算法1

(两次深度优先遍历) $O(n)$

1. 暴力算法很显然，每次枚举根结点，然后按照定义用一次深度优先遍历计算高度即可。这个过程中会有很多冗余计算，下面通过两次DFS来求出每个结点作为根结点的高度。
2. 不妨一开始假设 0 号结点为根结点，按照定义用一次遍历计算并记录每个结点拥有的最大高度，除根结点外，其他结点记录的最大高度是其作为子树根结点的最大高度。
3. 接下来，再用一次遍历，除 0 号结点外，求出其余结点从父结点传递到自身的最大高度。对于当前结点 u，其子结点 v 需要被传递的最大高度有两种选择，一种是从 u 父结点传递过来的最大高度，另一种是除了 v 以外，其余 u 的子结点含有的最大高度加 1。两种方式取最大值再加 1 即可得到 v 从 u 传递得到的最大高度。
4. 每个结点两次遍历中求出的最大高度取最大值即可得到每个结点作为根结点的最大高度。

时间复杂度

• 两次深度优先遍历，每个结点仅遍历两次次，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间建图，以及存储系统栈。

C++ 代码

class Solution {
public:

    void dfs_1(int u, int fa, vector<int>& max_height, vector<vector<int>>& tree) {
        max_height[u] = 0;
        for (auto &v : tree[u])
            if (v != fa) {
                dfs_1(v, u, max_height, tree);
                max_height[u] = max(max_height[u], max_height[v] + 1);
            }
    }

    void dfs_2(int u, int fa, vector<int>& max_height, vector<int>& t, vector<vector<int>>& tree) {
        max_height[u] = max(max_height[u], t[u]);
        int max_1 = 0, max_2 = 0; // 这里需要找子树中，最大高度的最大值和次大值，原因见 3 的解释。
        for (auto &v : tree[u])
            if (v != fa) {
                if (max_1 < max_height[v] + 1) {
                    max_2 = max_1;
                    max_1 = max_height[v] + 1;
                }
                else if (max_2 < max_height[v] + 1) {
                    max_2 = max_height[v] + 1;
                }
            }

        for (auto &v : tree[u])
            if (v != fa) {
                if (max_1 == max_height[v] + 1) {
                    t[v] = max(t[u], max_2) + 1;
                    dfs_2(v, u, max_height, t, tree);
                }
                else {
                    t[v] = max(t[u], max_1) + 1;
                    dfs_2(v, u, max_height, t, tree);
                }
            }
    }

    vector<int> findMinHeightTrees(int n, vector<pair<int, int>>& edges) {
        vector<vector<int>> tree(n);
        for (auto &e : edges) {
            tree[e.first].push_back(e.second);
            tree[e.second].push_back(e.first);
        }
        vector<int> max_height(n, 0), t(n, 0);
        dfs_1(0, -1, max_height, tree);
        // 第一次遍历记录每个结点在作为子树根结点的最大高度。

        dfs_2(0, -1, max_height, t, tree);
        // 第二次遍历补全每个结点作为总根结点的最大高度，差距就在于需要统计上从父结点传递过来的子树分支。

        int min_ans = n;
        vector<int> ans;
        for (int i = 0; i < n; i++)
            if (min_ans > max_height[i]) {
                min_ans = max_height[i];
                ans.clear();
                ans.push_back(i);
            }
            else if (min_ans == max_height[i]) {
                ans.push_back(i);
            }

        return ans;
    }
};

算法2

(贪心删点) $O(n)$

1. 从叶子结点开始，每一轮删除所有叶子结点。
2. 删除后，会出现新的叶子结点，此时再删除。
3. 重复以上过程直到剩余 1 个或 2 个结点，此时这 1 个或 2 个结点就是答案。

时间复杂度

• 每个点最多被访问 1 次，删除 1 次，所以时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间建图。

C++ 代码

class Solution {
public:

    vector<int> findMinHeightTrees(int n, vector<pair<int, int>>& edges) {
        if (n == 1)
            return vector<int>{0};

        vector<vector<int>> tree(n);
        vector<int> deg(n, 0);
        for (auto &e : edges) {
            tree[e.first].push_back(e.second);
            tree[e.second].push_back(e.first);
            deg[e.first]++;
            deg[e.second]++;
        }

        vector<int> res;
        for (int i = 0; i < n; i++)
            if (deg[i] == 1)
                res.push_back(i);

        while (n > 2) {
            vector<int> next_res;
            for (auto &u : res) {
                n--;
                for (auto &v : tree[u]) {
                    deg[v]--;
                    if (deg[v] == 1)
                        next_res.push_back(v);
                }
            }
            res = next_res;
        }

        return res;
    }
};