题目描述

给定一个二维矩阵matrix，请计算给定矩形区域内所有数的和，矩形区域由左上角坐标(row1, col1)和右下角坐标(row2, col2)给出。

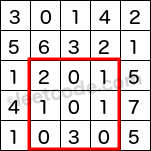
上图中给定的矩形区域是(2, 1) (4, 3)，它的数字和是8。

注意：

1. 你可以假定矩阵在询问过程中不会被修改；
2. sumRange()函数会被调用多次；
3. 数据保证 $row1 \le row2$ 且 $col1 \le col2$；

样例

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

算法

(前缀和) $初始化: O(n^2), sumRange: O(1)$

首先初始化出部分和数组f[N][N]，f[i][j]表示(i, j)左上部分区域的和。

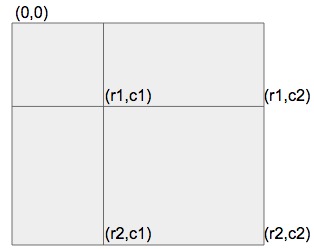
然后我们考虑如何计算矩形区域(row1, col1) (row2, col2)的和。
如下图所示，$S_{r1,c1,r2,c2} = S_{0,0,r2,c2} - S_{0,0,r1,c2} - S_{0,0,r2,c1} + S_{0,0,r1,c1}$;

时间复杂度分析：初始化要遍历整个矩阵，时间复杂度是 $O(n^2)$；计算矩形区域的和时只需要常数次计算，时间复杂度是 $O(1)$。

C++ 代码

class NumMatrix {
public:
    vector<vector<int>> f;

    NumMatrix(vector<vector<int>> matrix) {
        if (matrix.empty()) return;
        int n = matrix.size(), m = matrix[0].size();
        f = vector<vector<int>>(n + 1, vector<int>(m + 1, 0));
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= m; j ++ )
                f[i][j] = f[i - 1][j] + matrix[i - 1][j - 1];

        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= m; j ++ )
                f[i][j] += f[i][j - 1];
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return f[row2 + 1][col2 + 1] - f[row2 + 1][col1] - f[row1][col2 + 1] + f[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */