题目描述

一共有n个数，编号是1~n，最开始每个数各自在一个集合中。

现在要进行m个操作，操作共有两种：

“M a b”，将编号为a和b的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
“Q a b”，询问编号为a和b的两个数是否在同一个集合中；
输入格式
第一行输入整数n和m。

接下来m行，每行包含一个操作指令，指令为“M a b”或“Q a b”中的一种。

输出格式
对于每个询问指令”Q a b”，都要输出一个结果，如果a和b在同一集合内，则输出“Yes”，否则输出“No”。

每个结果占一行。

数据范围
1≤n,m≤105
输入样例：
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例：
Yes
No
Yes

关注我，不迷路~~

思路

并查集
从代码的角度分析

初始化

for(int i = 0; i < 8; i ++) p[i] = i;

上面的代码实现的结果如下图所示

很容易理解，就是将当前数据的父节点指向自己

查找 + 路径压缩

int find(int x){ //返回x的祖先节点 + 路径压缩
    //祖先节点的父节点是自己本身
    if(p[x] != x){
        //将x的父亲置为x父亲的祖先节点,实现路径的压缩
        p[x] = find(p[x]);    
    }
    return p[x]; 
}

find的功能是用于查找祖先节点，那么路径压缩又是怎么完成的

注意图，当我们在查找1的父节点的过程中,路径压缩的实现

针对 x = 1

find(1) p[1] = 2  p[1] = find(2)
find(2) p[2] = 3  p[2] = find(3)
find(3) p[3] = 4  p[3] = find(4)
find(4) p[4] = 4  将p[4]返回

退到上一层
find(3) p[3] = 4  p[3] = 4 将p[3]返回
退到上一层
find(2) p[2] = 3  p[2] = 4 将p[2]返回
退到上一层
find(1) p[1] = 2  p[1] = 4 将p[1]返回

至此，我们发现所有的1，2，3的父节点全部置为了4，实现路径压缩；同时也实现了1的父节点的返回
nice!!

合并操作

if(op[0] == ‘M’) p[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点
假设有两个集合

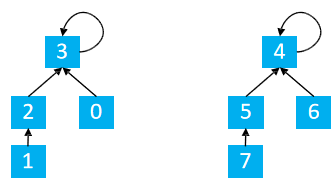
合并1， 5
find(1) = 3 find(5) = 4
p[find(1)] = find(5) –> p[3] = 4
如下图所示

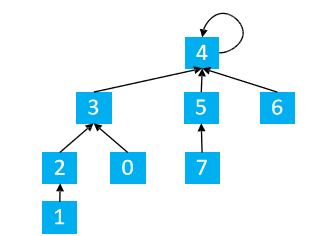
查找

find(a) == find(b) 这很简单，就不介绍了

其他路径压缩方法

1 路径分裂：使路径上的每个节点都指向其祖父节点（parent的parent）

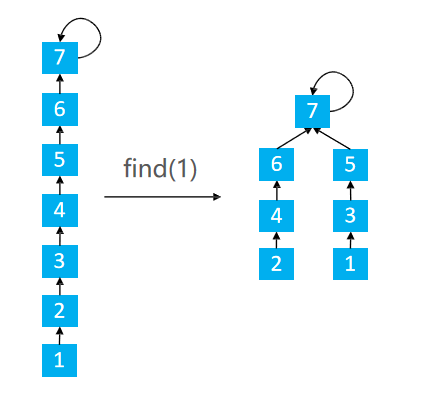
int find(int x){
    while(x != p[x]){
        int parent = p[x];
        p[x] = p[p[x]];
        x = parent;
    }
    return x;
}

2 路径减半：使路径上每隔一个节点就指向其祖父节点（parent的parent）

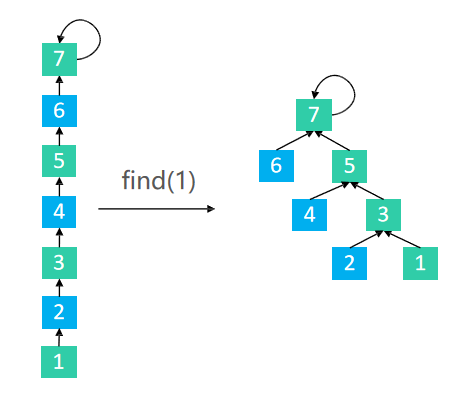
int find(int x){
    while(x != p[x]){
        p[x] = p[p[x]];
        x = p[x];
    }
    return x;
}

总结

并查集
1.将两个集合合并
2.询问两个元素是否在一个集合中

基本原理：每个集合用一棵树来表示。树的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点

1.判断树根 if(p[x] = x)
2.求x的集合编号 while(p[x] != x) x = p[x]
3.合并两个集合，这两将x的根节点嫁接到y的根节点, px为x的根节点， py为y的根节点，嫁接p[px] = py

java

import java.util.*;

public class Main{
    static int n, m;
    static int N = 100010;
    static int[] p = new int[N];


    public static int find(int x){
        if(x != p[x]) p[x] = find(p[x]);
        return p[x];
    }

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();

        for(int i = 0; i < n; i ++) p[i] = i;

        String opt;
        int a, b;
        while(m -- > 0){
            opt = sc.next();
            a = sc.nextInt();
            b = sc.nextInt();
            if(opt.equals("M")) p[find(a)] = find(b);
            else{
                if(find(a) == find(b)) System.out.println("Yes");
                else System.out.println("No");
            }
        }
    }
}

python3

N = 100010
p = [0] * N

def find(x):
    global p
    if(x != p[x]): p[x] = find(p[x])
    return p[x]

def main():
    global p
    n, m = list(map(int, input().split(" ")))
    for i in range(n):
        p[i] = i

    while(m):
        m -= 1
        opt, a, b = list(input().split(" "))
        a = int(a)
        b = int(b)
        if(opt == 'M'):
            p[find(a)] = find(b)
        else:
            if(find(a) == find(b)):
                print("Yes")
            else:
                print("No")

main()

c++

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N];

int find(int x){ //返回x的祖先节点 + 路径压缩
    //祖先节点的父节点是自己本身
    if(p[x] != x){
        //将x的父亲置为x父亲的父亲,实现路径的压缩
        p[x] = find(p[x]);    
    }
    return p[x]; 
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++) p[i] = i; //初始化，让数x的父节点指向自己
    while(m --){
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);

        if(op[0] == 'M') p[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点
        else{
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}