3. 最长公共子序列
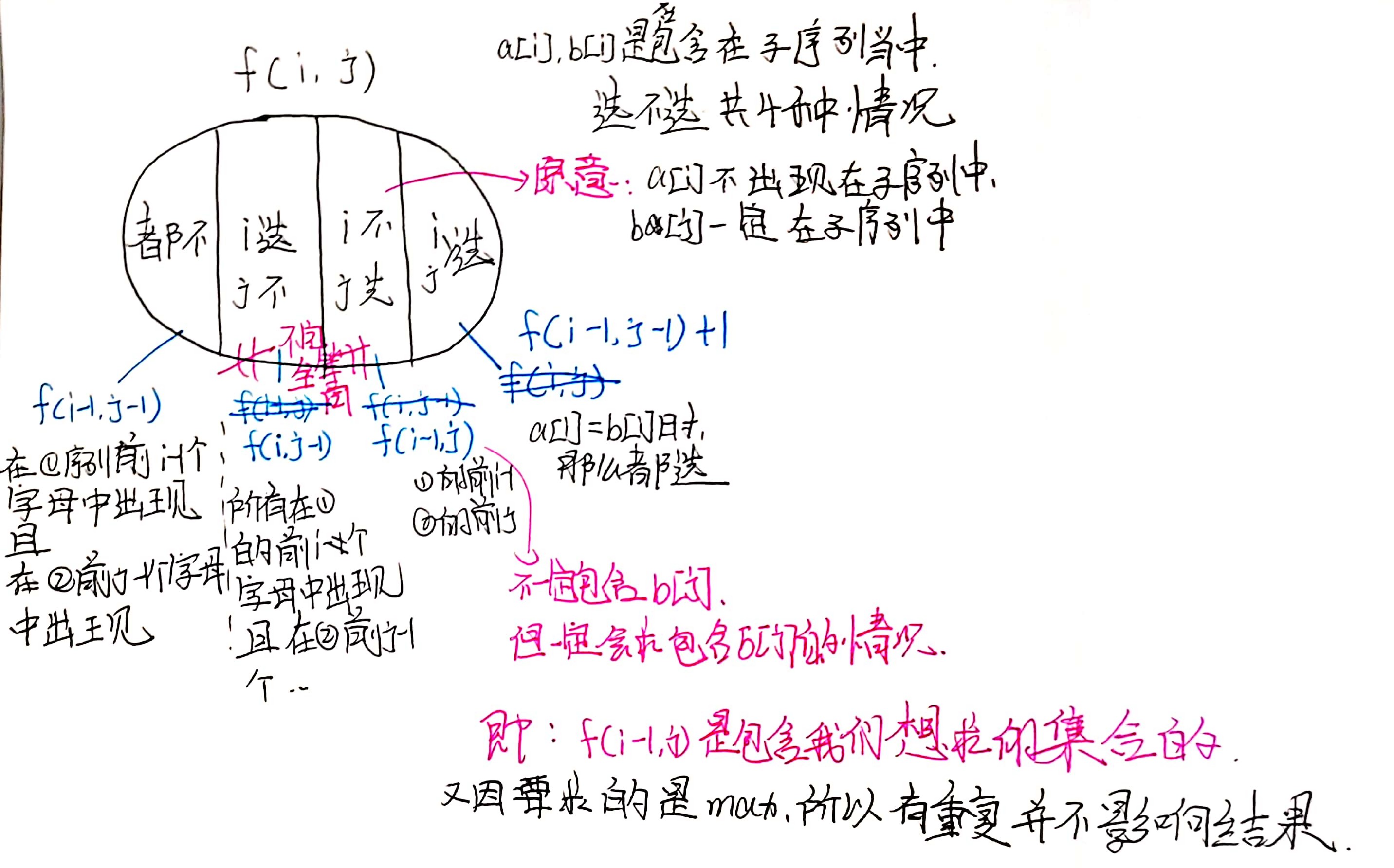
| $f[i][j]$——集合:所有在第一个序列的前$i$个字母中出现,且在第二个序列的前$j$个字母中出现的子序列 |
|---|
| 属性:最大值 |
递归版:
或许也不需要那么费力想,先以递归的思想——枚举。
共有4种情况:都不选,其中一个选(2种),都选($a[i] == b[i]$)。
-
a[i]选,b[j]不选:直接看dfs(i ,j + 1)即可,若仔细想想dfs(i ,j + 1)的情况其实有很多,并不是我们想的b[j]一定不选而是继续对
a的后i+1的个和b的后j个进行这4种情况的判断。这4种情况
包含了a[i]选,b[j]不选,这种情况,由于是取max,故并不影响。 -
a[i]不选,b[j]选:和1一样。 -
都不选其实是包含在
12中的,比如:a[i]选,b[j]不选,然后继续递归到
ij+1, 会继续判断上面说的几种情况判断,其中一种:
a[i]不选,b[j+1]选。那么到这,a[i]b[j]都不选的情况是判断了的。故不需要单独判断都不选的情况。
先食用递归版,然后用递归方程来理解与推出循环版
#include <iostream>
#include <algorithm>
using namespace std;
const int n = 1010;
char a[n], b[n];
int f[n][n];
int N, M;
int dfs(int i, int j)
{
if (i == N + 1 || j == M + 1)
return 0;
if (f[i][j])
return f[i][j];
int res = 0;
// 若相等 则一定都选
if (a[i] == b[j])
res = 1 + dfs(i + 1, j + 1);
else
// 不选a[i]选b[j] , 选a[i]不选b[j]
res = max(dfs(i + 1, j), dfs(i, j + 1));
return f[i][j] = res;
}
int main()
{
cin >> N >> M;
scanf("%s%s", a + 1, b + 1);
cout << dfs(1, 1);
cout << endl;
// f矩阵
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
cout << f[i][j] << ' ';
cout << endl;
}
return 0;
}
循环版:
理解了递归版,看一下DP方程,就很好理解啦~
🐷
#include <iostream>
#include <algorithm>
using namespace std;
const int n = 1010;
char a[n], b[n];
int f[n][n];
int main()
{
int N, M;
cin >> N >> M;
scanf("%s%s", a + 1, b + 1);
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++)
{
if (a[i] == b[j])
f[i][j] = f[i - 1][j - 1] + 1;
else
f[i][j] = max(f[i][j - 1], f[i - 1][j]);
}
cout << f[N][M];
return 0;
}