题目描述

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.

Example 1:

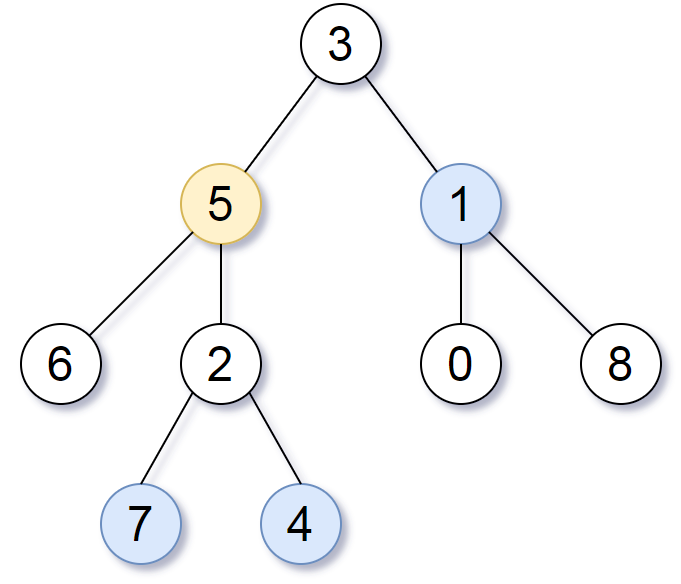
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
Output: [7,4,1]
Explanation: 
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.
Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

Note:

1. The given tree is non-empty.
2. Each node in the tree has unique values 0 <= node.val <= 500.
3. The target node is a node in the tree.
4. 0 <= K <= 1000.

题意：给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

算法1

保存路径

题解：首先第一遍dfs找到目标节点并保存路径。然后从以目标节点为根节点向下dfs$K$层，再以父节点 $K-1$层，再以父节点的父节点向下dfs $K - 2$层。

这里注意如果当点节点需要向下递归$dist$层:

• $dist < 0$，需要跳出循环了
• $dist = 0$，保存当前节点当作答案
• $dist = K$，也就是target节点，直接向下dfs
• 否则，当前节点有两个孩子节点，选择其中不在路径上的孩子节点，向下遍历$dist -1$层

C++ 代码

class Solution {
public:
    vector<TreeNode*> path;
    vector<int> res;
    vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
        dfs(root,target);// 保存从根节点到当前节点的路径
        int level = path.size();
        for(int i = path.size() - 1 ;i >= 0 ;i --)
        {       //  计算需要向下遍历的距离
            int dist = K + i + 1 - level;
            if(dist < 0)
                break;
            else if(dist == 0)
                res.push_back(path[i]->val);
            else if(dist == K)
                dfs_1(path[i],0,dist);
            else 
            {
                //  判断应该从左孩子开始遍历，还是右孩子
                bool ifLeft = (path[i + 1] == path[i]->left);
                if(ifLeft)
                    dfs_1(path[i]->right,0,dist - 1);
                else
                    dfs_1(path[i]->left,0,dist - 1);
            }
        }
        return res;
    }
    //  从当前节点开始找到所有相对深度为dist的节点
    void dfs_1(TreeNode* root,int level,int dist)
    {

        if(root == NULL)
            return;
        if(level == dist){
            res.push_back(root->val);
            return;
        }
        dfs_1(root->left,level + 1,dist);
        dfs_1(root->right,level + 1,dist);   
    }
    //  查找并保存路径，也可以用非递归后序遍历来写
    bool dfs(TreeNode* root,TreeNode* & target)
    {
        if(root == NULL)
            return false;
        path.push_back(root);
        if(root == target)
            return true;
        if(dfs(root->left,target)) return true;
        if(dfs(root->right,target)) return true;
        else {
            path.pop_back();
            return false;
        }    
    }
};