算法基础班–第二章–8.Trie树模板

算法模板

int son[N][26], cnt[N], idx;
char str[N];

// p 下标是p的点， p点的所有儿子都存在了son[p]中，
// son[p][0] son[p][1] 分别表示p的第一个儿子，第二个儿子…
// cnt[x]以x结尾的单词数量有多少个

// 插入一个字符串
void insert(char str[]) {
    int p = 0; 
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])  son[p][u] = ++idx;  
        p = son[p][u];
    }
    cnt[p]++; 
}

//查询字符串出现的次数
int query(char* str) {
    int p = 0; 
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])  return 0; 
        p = son[p][u];
    }
    return cnt[p]; 
}

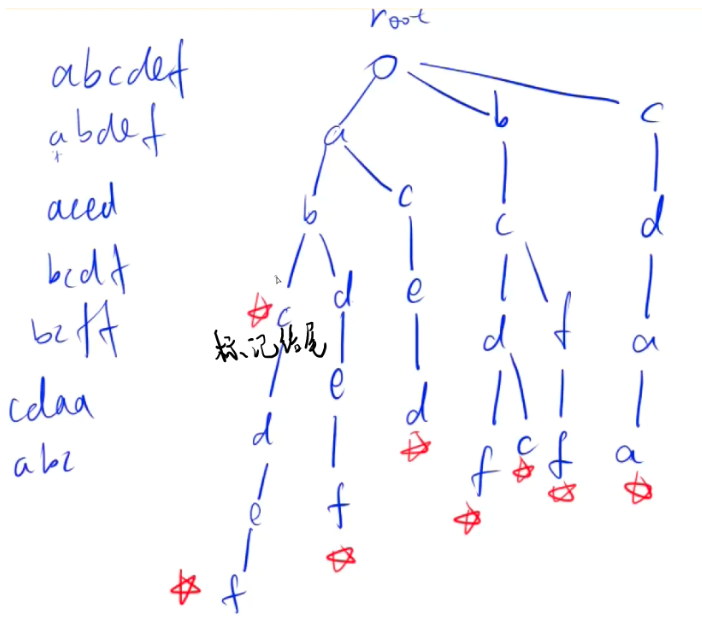
这里的☆就相当于代码中cnt[p]
要对每个字符串结尾的字母标记，比如abc，否则还以为abc不是Trie树中的元素，标记方式就是cnt[p]
不一定非得是叶子节点才能表☆，只要是字符串结尾的字母都表☆，有多少个不同的字符串就有多少个☆。

本题完整代码

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 100010;
int son[N][26], cnt[N], idx;
char str[N];
// p 下标是p的点， p点的所有儿子都存在了son[p]中，
// son[p][0] son[p][1] 分别表示p的第一个儿子，第二个儿子...
// cnt[x]以x结尾的单词数量有多少个

// 插入字符串
void insert(char str[]) {
    int p = 0; //从根节点开始，从前往后遍历
    for (int i = 0; str[i]; i++) {//因为字符串结尾时'\0'，用'\0'判断字符串是否走到结尾
        int u = str[i] - 'a'; // 每次求出当前字母对应的子节点编号（0~25）
        if (!son[p][u])  son[p][u] = ++idx; //如果当前节点不存在对应“字母”，则创建出来。 p这个节点不存在u号这个儿子，则创建出来
        p = son[p][u]; // p向下更新（如果是走if下来的，则更新为刚创建的点,否则将当前父节点更新为该字符串对应p的儿子节点）（好难描述！）
    }
    cnt[p]++; //往字符串中插入结束时，p对应的点就是该字符串上最后一个点,cnt[p++]表示☆处，以这个点☆结尾的单词数量多了一个。
    //另外cnt[i]中要么是0或1，要么是同一个字符串出现的次数
}

int query(char str[]) {
    int p = 0; //从根节点开始，从前往后遍历
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])  return 0; //如果不存在该子节点，直接return 0;不做插入处理，因为是查询
        p = son[p][u]; //存在该店，更新为子节点的编号
    }
    return cnt[p]; //返回字符串中出现的次数（返回以p结尾的单词数量）
}

int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        char op[2];
        scanf("%s%s", op, str);
        if (op[0] == 'I') insert(str);
        else printf("%d\n", query(str));
    }
    return 0;
}