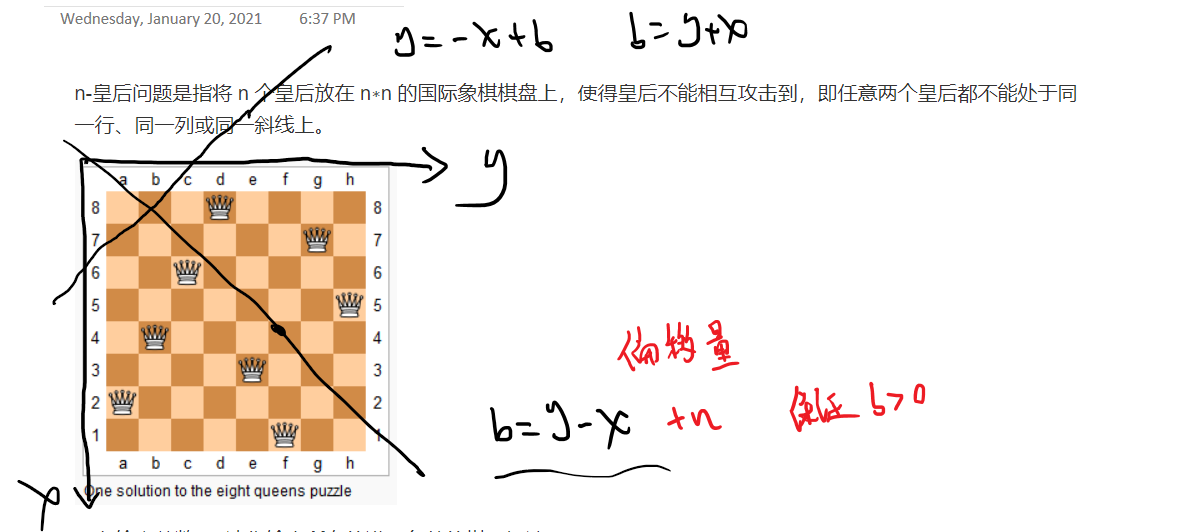
做法一

/*
 * Project: DFS
 * File Created:Wednesday, January 20th 2021, 6:43:58 pm
 * Author: Bug-Free
 * Problem: AcWing 843. n-皇后问题
 */
#include <iostream>

using namespace std;

const int N = 10;

int n;
bool col[N], dg[N * 2], udg[N * 2];
char g[N][N];

void dfs(int u) {
    if (u == n) {
        for (int i = 0; i < n; i++) {
            puts(g[i]);
        }
        puts("");
        return;
    }
    for (int i = 0; i < n; i++) {
        //只要保证不同对角线会对应到不同数组下标即可
        if (!col[i] && !dg[n - u + i] && !udg[u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[n - u + i] = udg[u + i] = true;
            dfs(u + 1);
            col[i] = dg[n - u + i] = udg[u + i] = false;
            g[u][i] = '.';
        }
    }
}

int main() {
    cin >> n;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = '.';
        }
    }

    dfs(0);

    return 0;
}

做法二

/*
 * Project: DFS
 * File Created:Wednesday, January 20th 2021, 10:31:28 pm
 * Author: Bug-Free
 * Problem: AcWing 843. n-皇后问题
 */
#include <iostream>

using namespace std;

const int N = 10;

int n;
bool row[N], col[N], dg[N], udg[N];
char g[N][N];

// 行, 列, 总皇后数
void dfs(int x, int y, int s) {
    if (s > n) {
        return;
    }
    if (y == n) {
        //列变为0, 行+1
        y = 0, x++;
    }
    if (x == n) {
        if (s == n) {
            for (int i = 0; i < n; i++) {
                puts(g[i]);
            }
            puts("");
        }
        return;
    }
    // 不放的分支
    dfs(x, y + 1, s);  //往右边, 列+1

    // 放的分支
    if (!row[x] && !col[y] && !dg[n + y - x] && !udg[x + y]) {
        row[x] = col[y] = dg[n + y - x] = udg[x + y] = true;
        g[x][y] = 'Q';
        dfs(x, y + 1, s + 1);
        g[x][y] = '.';
        row[x] = col[y] = dg[n + y - x] = udg[x + y] = false;
    }
}

int main() {
    cin >> n;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = '.';
        }
    }

    dfs(0, 0, 0);

    return 0;
}