@[一维优化在底下]

二维DP

闫氏DP分析法：

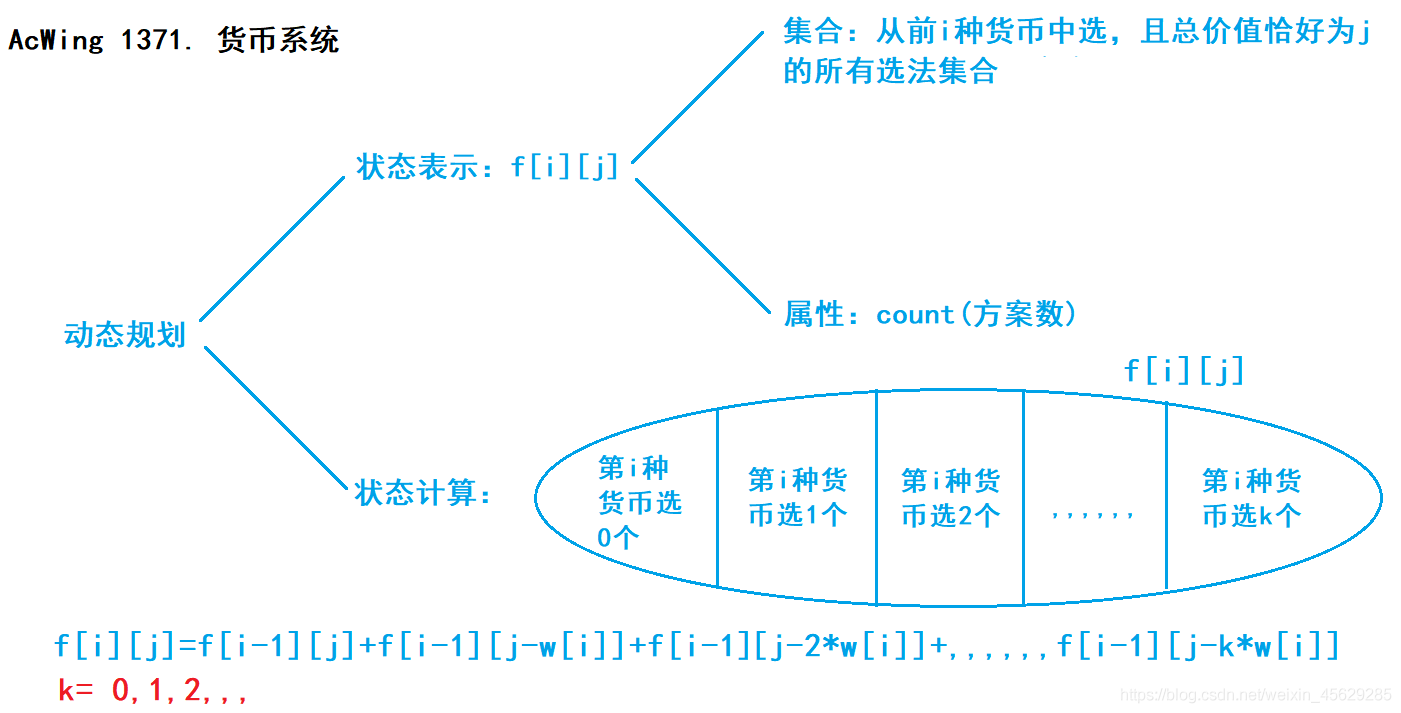
状态表示： f[i][j] 表示 从前i种货币中选，且总价值恰好为j的所有选法集合的方案数。

那么f[n][m]就表示表示 从前n种货币中选，且总价值恰好为m的所有选法集合的方案数，即为答案。

集合划分：

按照第i种货币可以选 0个,1个，2个，3个，，，，k个划分集合 f[i][j]。其中k*w[i] <= j,也就是说在背包能装下的情况下，枚举第i种货币可以选择几个。

状态计算：

f[i][j] = f[i-1][j]+f[i-1][j-w[i]]+f[i-1][j-2*w[i]],,,,,,+f[i-1][j-k*w[i]] .

ac代码

#include<iostream>
#include<cstdio>

using namespace std;
const int N = 30,M = 1e4 +10;
long long  f[N][M]; // 方案数很大使用long long 来存
int w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i <= n; i++) cin>>w[i];

    f[0][0] = 1; // 使用0种货币，凑0元钱,也是一种方案

    for(int i = 1; i <= n; i++)
      for(int j = 0; j <= m; j++)
      {
          for(int k = 0; k*w[i] <= j; k++)
            f[i][j] += f[i-1][j-k*w[i]];    //状态计算方程
      }      
    cout<<f[n][m]<<endl;
    return 0;
}

一维DP

考虑优化

v代表第i件物品的体积(面值)

f[i][j] = f[i-1][j] + f[i-1][j-v]+f[i-1][j-2v]+,,,,,+f[i-1][j-kv])

f[i][j-v] = f[i-1,[j-v]+f[i-1][j-2v]+,,,,,+f[i-1][j-kv])

因此：

f[i][j] = f[i-1][j]+f[i][j-v])

图示：

去掉一维：

状态计算方程为： f[j] = f[j] + f[j-v]

ac代码

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e4 + 10;
long long f[N];
int main()
{
    int m,n;
    cin>>n>>m;
    f[0] = 1;  //初始化 f[0][0] = 1 
    for(int i = 1; i <= n; i++)
    {
        int v;
        cin>>v;
        for(int j = v; j <= m; j++)
          f[j] += f[j-v];   // 状态计算方程
    }
    cout<<f[m]<<endl;
    return 0;
}