n-皇后问题
题目描述
n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数n，请你输出所有的满足条件的棋子摆法。
输入格式
共一行，包含整数n。
输出格式
每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。
其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。
每个方案输出完成后，输出一个空行。
数据范围
1≤n≤9
样例
输入样例：
4
输出样例：
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
算法1 最新清晰写法
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行，故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
// 枚举u这一行，搜索合法的列
int x = u;
for (int y = 0; y < n; y ++ )
// 剪枝(对于不满足要求的点，不再继续往下搜索)
if (col[y] == false && dg[y - x + n] == false && udg[y + x] == false) {
col[y] = dg[y - x + n] = udg[y + x] = true;
g[x][y] = 'Q';
dfs(x + 1);
g[x][y] = '.'; // 恢复现场
col[y] = dg[y - x + n] = udg[y + x] = false;
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
算法1（旧的写法）
过去的写法（DFS按行枚举） 时间复杂度$O(n!)$
代码分析
对角线 $dg[u + i]$，反对角线$udg[n - u + i]$中的下标 $u + i$和 $n - u + i$ 表示的是截距
下面分析中的$(x, y)$相当于上面的$(u, i)$
- 反对角线 $y = x + b$, 截距 $b = y - x$，因为我们要把 $b$ 当做数组下标来用，显然 $b$ 不能是负的，所以我们加上 $+n$ （实际上+n+4,+2n都行），来保证是结果是正的，即 y - x + n
- 而对角线 $y = -x + b$, 截距是 $b = y + x$，这里截距一定是正的，所以不需要加偏移量
核心目的：找一些合法的下标来表示$dg$或$udg$是否被标记过，所以如果你愿意，你取 $udg[n + n - u + i]$ 也可以，只要所有$(u, i)$对可以映射过去就行
C++ 代码
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行，故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点，不再继续往下搜索)
// udg[n - u + i]，+n是为了保证下标非负
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
g[u][i] = '.';
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
算法2
（DFS按每个元素枚举）时间复杂度$O(2^{n^2})$
时间复杂度分析：每个位置都有两种情况，总共有 $n^2$ 个位置
C++ 代码
// 不同搜索顺序 时间复杂度不同 所以搜索顺序很重要！
#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row
// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
// 处理超出边界的情况
if (y == n) y = 0, x ++ ;
if (x == n) { // x==n说明已经枚举完n^2个位置了
if (s == n) { // s==n说明成功放上去了n个皇后
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
}
return;
}
// 分支1：放皇后
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
g[x][y] = '.';
}
// 分支2：不放皇后
dfs(x, y + 1, s);
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
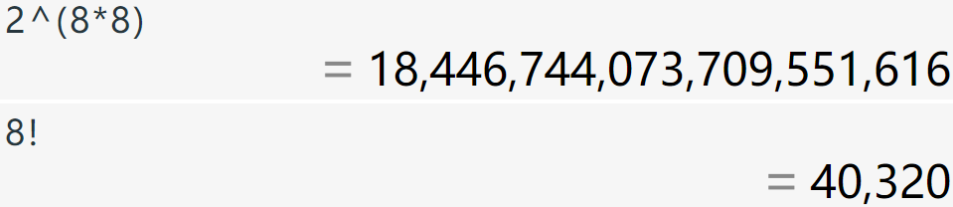
按元素位置枚举是要比按位置枚举慢很多的：
我的只使用一维，更为简洁清晰，如有用，还请大家到我的题解点个赞，让更多人看到，谢谢。
好优秀
同样的思路nice
图中有几个错误,
i和u的范围是取不到端点的:$(y -x) \in (-n, n)$.
$(n + y - x) \in (0, 2*n)$.
$(y + x) \in (0, 2n)$.
请问，为什么取不到端点呀
因为x和y的起始坐标为0，第零行最右侧的点为(0,n-1)，此时b最大为n-1而不是n
哦哦，谢谢哦
我在老家，没网没WIFI，为了收藏这视频，天刚刚亮我便出发了，我走了几十公里的山路来到镇上，脚上磨起了许多豆大的水泡，鞋子也开胶了。本来想把家里的苞谷卖掉几十斤，在镇上坐车到城里的网吧收藏这篇文章的，无奈天公不作美，今年收成不好，种的粮食只够家里吃，所以我只好在镇上的砖窑里打工，挣足路费。从砖窑搬一块砖到拖拉机上只给一分钱，为了100块的车费，我搬了一万块砖，十个手指头都磨出了鲜血，为了省下车费，我没贴云南白药创可贴，让血液自然凝结。之后拿到搬砖钱，我坐上了从镇上开往城里的汽车。来到网吧，一摸兜里，我淦，没有三块钱的上网费了，少搬了300块砖。我只好在大街上四处奔走，守望着那些喝矿泉水的人们，当他们将矿泉水瓶从手中抛出的那一刹那，我就像守门员扑球般扑去了，生怕矿泉水瓶被别人抢去了。因为要是那样，我收藏这篇文章又会晚上那么几秒钟，你理解我迫不及待的心情么？历尽千辛万苦，我终于收集到60个珍贵的矿泉水瓶子，想拿到废品收购站换了3块钱的网费，奈何废品收购站在城郊，离网吧十分远，我已没有多余的钱坐车，只能跋涉六个小时，摸着黑去。回到网吧，天色已渐渐发亮，终于收藏了你的这视频。欢迎回访！
0.0
0.0
hhhhhhh
查重率百分之百
qwq
确实，与多款音乐软件内多人多条评论完全相同…
算法1写的很棒
好难呀，我人晕了
亲测，放皇后中的dfs（x,y+1,s+1)改为dfs（x+1,0,s+1)会更快
因为这一行已经放过皇后了 直接可以跳过该行的枚举，直接枚举下一行
y总说了第二种是一个位置一个位置搜的，不考虑剪枝。
确实，这个代码更为高效👍
它不是从后往前放吗，不应该是（x-1,0,s+1）吗，搞不懂
大佬，为啥我把数组改成从1开始就不对了呢
从1开始，puts(g[i])会有点问题，你两重循环输出g[i][j]吧
soga, 我明白了！没注意到这个，谢谢大佬！
还有应该是u==n+1吧
对的，数组从一开始，当时忘记改了
不太明白 有啥问题呀
感谢感谢！
为什么从1开始，puts（g[i]）会有问题
为什么是u= n+1呢
为什么u==n+1呢
因为char的第0个字符转换成数字是0，是个控制字符（理解成看不见的字符就行啦），然后就会输出一个类似空格的东西
因为你之前从0开始是0~n，从1开始不就是1~n+1吗？如果是从1~n的话就少枚举了一个
也可以这么说，puts是从第0个字符开始输出，一直输出到结束
然后就会多出来一个
因为puts(g[i])每行都是从0开始输入的，所以从1开始的话要注意横纵坐标的不同。
把u和i替换成x 和y好理解很多，谢谢博主！！
大佬，问一下，这里定义的二维g[i][j],但是输出的一维g[i]，为什么不影响呀？
g[i][i]是char型，输出g[i]相当于char*，也就是输出字符串
相当于输出一行吗
对，相当于输出一行，这个和指针相关，可以去看看puts的传入参数就知道了
char*不一定是字符串哦
还会是什么呀
还有可能只是一个指针，也可以是字符串指针
%%%
puts(g[i])等效于printf(“%s\n”,g[i])。g[i][i]是char型，输出g[i]相当于char*,
这会将连续的地址上的储存的字符输出，遇到’\0’（结束符）时就停止输出，由于N>n，
也就是每次输出行时必有结束符，所以就能用这种方式输出整个二维数组。
题解里好像并没有结束符，为什么还能实现呢
怎么说呢，因为字符串的最后会自动补一个结束符，而且就算你自己加了结束符，他也只会把你的结束符当成一个空格而已，因为实际上字符串有自己的结束符
‘\0’不是结束符哦，结束符其实是EOF，不过输出出现问题的时候也会返回EOF的
uu，我后来发现全局变量的char类型会默认初始化为’\0’， 所以其实确实是存在’\0’的呢
你很聪明嘛！
大佬，我想请问一下，如果这题从1开始的话，u为什么等于n+1才是对的呢
因为实际上是只经过n次就可以的到结果，+1是为了输出结果
从dfs(1)开始的话意味着g矩阵起点为（1，1），终点为（n,n）；函数递归调用dfs(1),dfs(2)…dfs(n)依次给1到n行设置皇后,在dfs(n)中成功通过if语句给第n行设置了皇后g[u][y]=’Q’;之后，会调用dfs(u+1)，此时的u等于n，也即dfs(n+1),则使结束递归条件为u==n+1，在dfs(u+1)中结束递归。
算法二
if(y==n) x++,y=0;如果写在if(x==n)后面为啥结果就不对了呢
先在dfs函数开头加上一段 cout << “x:” << x << “y:” << y << “s:” << s << endl;
然后令n=1.得到输出
/x:0y:0s:0
x:0y:1s:0 本来本次dfs应该先执行换行，使得x变成1，y变成0，然后再执行if(n==x)回溯。但是修改后先判断if(n==x)不满足回溯条件，再使x变成1，y变成0，多进入了两个分支
x:1y:1s:0
x:1y:1s:1 这个分支不在nn的范围内，错误
.
*/
谢谢大佬 虽然我后面看懂了哈哈
你好，请问以下，为什么输出直接g[i]，就可以输出完整的图， 我在别的地方弄个二维字符数组，然后输出g[0]是直接把一整串字符都输出去了， 为什么这题这样写，就可以输出完整的图
你要注意 这个是要u==n的时候才能输出，我理解你的意思，一个字符数组输出a[0]，是将连续的地址上的存储字符输出，<n，没有取到n 留了一个’\0’结束符，这样就可以输出了。
为什么要将b当作数组下标来用？不理解这个操作
要确定正对角线和反对角线都没有皇后, 对角线数组可以看成是第几条对角线, 这样可能更好理解, 而要看第几条对角线的话就要用u和i来算
我明白了，在同一条直线上，x,y是不同的但是b是相同的，所以确定b就确定x,y了
u和i确定b，b是在不断变化的, 我个人把它理解成
第几条对角线大佬，第一种搜索顺序为什么是O(n!)
可以详细解释下吗？
我怎么觉得是O(n^n)呢？
第一行可以有n个位置可选，第二行只剩n-1个位置可选，依次类推。 我也不太确定， 递归的时间复杂度都不太好想。
可是for循环固定执行n次呀
是执行n次，但是到了下一层就执行(n - u + 1)n次了，然后如此类推，会发现越到下一层就越少，最后到最后一层应该是1n了。
//对n个位置按行搜索 应该是按列搜索吧
dfs(0) 调用了 n次 dfs(1)
dfs(1) 调用了 n-1次 dfs(2)
…
dfs(n - 1) 调用了 1次dfs(n)
讨论一下这个理解
相比于for循环，更应该关注进入了几次dfs，因为递归子函数要比一个if判断复杂度高得多。。。另外你可以在dfs开头加个cnt，看看总共进行了多少次递归
n开9也能过啊
太棒啦
为什么要恢复现场来着？
为什么代码运行出来会有不同种的情况