LeetCode 236. 二叉树的最近公共祖先

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

LeetCode 236. 二叉树的最近公共祖先原题链接中等

作者：

wzc1995 , 2018-06-10 10:33:20 , 所有人可见 , 阅读 4282

27

11

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

样例

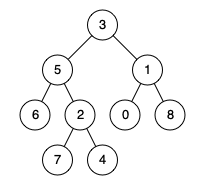
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：结点 5 和结点 1 的最近公共祖先是结点 3。

binarytree (1).png .png)

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：结点 5 和结点 4 的最近公共祖先是结点 5。因为根据定义最近公共祖先结点可以为结点本身。

输入：root = [1,2], p = 1, q = 2
输出：1

注意

树中节点数目在范围 [2, 10^5] 内。
-10^9 <= Node.val <= 10^9
所有 Node.val 互不相同。
p != q
p 和 q 均存在于给定的二叉树中。

算法

(DFS) $O(n)$

此题与 Lowest Common Ancestor of a Binary Search Tree 最大的不同就是这道题给定的二叉树不再是二叉查找树。
所以我们需要通过遍历整棵树，分别找到 p 和 q 结点到根结点的路径，然后枚举匹配路径上的点找到最近公共祖先。
遍历的算法采用的深度优先搜索，搜索时，需要一个数组记录路径；在每一层尝试两个方向的路径，如果某一个方向找到了目标结点或者当前点就是目标结点，则当且结点加入数组，并返回 true；否则返回 false。
最后根据两个数组的路径，找到最低的公共结点即可。

时间复杂度

由于需要遍历整棵树，每个结点仅遍历两次，故时间复杂度为 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    bool dfs(TreeNode *cur, TreeNode *des, vector<TreeNode*> &path_node) {
        if (cur == NULL)
            return false;
        if (cur == des) {
            path_node.push_back(cur);
            return true;
        }
        if (dfs(cur -> left, des, path_node) || dfs(cur -> right, des, path_node)) {
            path_node.push_back(cur);
            return true;
        }

        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path_node_p, path_node_q;
        dfs(root, p, path_node_p);
        dfs(root, q, path_node_q);
        reverse(path_node_p.begin(), path_node_p.end());
        reverse(path_node_q.begin(), path_node_q.end());

        int n = min(path_node_p.size(), path_node_q.size());
        for (int i = n - 1; i >= 0; i--)
            if (path_node_p[i] == path_node_q[i])
                return path_node_p[i];

        return NULL;
    }
};

18 评论

这是空格 2023-03-23 23:23

不需要逆转,直接从后往前遍历找到最后一个相同的
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> pathp;
        vector<TreeNode*> pathq;

        dfs(root,p,pathp);
        dfs(root,q,pathq);
        // for(int i=0;i<pathp.size();i++){
        //     cout<<pathp[i]->val<<endl;
        // }
        // for(int i=0;i<pathq.size();i++){
        //     cout<<pathq[i]->val<<endl;
        // }
        int m=pathp.size();
        int n=pathq.size();

        TreeNode* res=NULL;

        for(int i=m-1,j=n-1;;j--,i--){

            if(j<0 || i<0 || pathp[i]!=pathq[j]){
                break;
            }
            res=pathp[i];
        }

        return res;
    }
    bool dfs(TreeNode* cur,TreeNode* tar,vector<TreeNode*>& path){
        if(cur==NULL)return false;
        if(cur==tar){
            path.push_back(cur);
            return true;
        }
        if(dfs(cur->left,tar,path) || dfs(cur->right,tar,path)){
            path.push_back(cur);
            return true;
        }
        return false;
    }

Tie 2019-09-25 13:03

这里为什么还要reverse一下，直接for ( i = 0; i < n - 1; i ++ )不可以么

Tie 2019-09-25 13:15

好像懂了，path_p 和path_q 的size不一样，找path_p[i] == path_q[i]的时候要多考虑一下

IShowMeat 11个月前

LCA问题，一次查找，考虑向上标记法！！

再疯狂一次吧 2021-11-24 20:50

太赞了！

lial 2021-05-30 14:52

讲的很好，赞！

AcGrt 2020-03-29 22:41

学习了讲得超好

Omega_ 2020-02-28 21:06

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr || root == p || root == q){return root; }
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        return left == nullptr? right : (right == nullptr? left : root); 
    }

我这个的思路和您在二叉搜索树那个版本答案的思路完全一致啊= = 您为什么这道题要搞这么大的工程= =

wzc1995 2020-02-29 09:30

这两道题的思路完全不一样，你这个只是在形式上简化了我的代码

Omega_ 2020-02-29 13:53 回复了 wzc1995 的评论

好吧我懂了 - -想少了之前

天才小笼包 2021-05-28 04:18 回复了 Omega_ 的评论

两位前辈好，我也是用了 @Heisenberg_ 的解法直接递归，我理解 @wsc1995 的方法是找到从根节点root 到p的path ，及从root到q的path，然后两个path找第一个common node就是公共祖先（错了请指正），但是为什么@Heisenberg_ 只是形式化简化了这个代码呢？谢谢！

wzc1995 2021-05-29 17:15 回复了天才小笼包的评论

两个写法在本质上是一致的，都是定位到两个结点所在的位置，最坏情况都需要遍历整棵树

Omega_ 2020-02-28 21:03

为什么不能像二叉搜索树一样递归呢不是一样的吗

wzc1995 2020-02-29 09:33

按照你的写法当然可以，但时间和空间复杂度仍然是 $O(n)$，不可能像二叉搜索树那道题降到 $O(h)$。

TripleU 2019-08-05 14:26

这个题，不知道为什么我的运行时间特别长，感觉算法复杂度都哦一样的啊

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':

        ret = [None] * 2

        def func(_root, p, q, path):

            if not _root:
                return
            if _root.val == p.val:
                ret[0] = path + [_root]
            elif _root.val == q.val:
                ret[1] = path + [_root]

            if ret[0] and ret[1]:
                return

            func(_root.left, p, q, path + [_root])
            func(_root.right, p, q, path + [_root])

        func(root, p, q, [])

        i = 0

        while i < len(ret[0]) and i < len(ret[1]) and ret[0][i] == ret[1][i]:
            i +=1

        return ret[0][i-1]