题目描述

给定一个二叉搜索树的根节点 root，和一个整数 k，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

样例

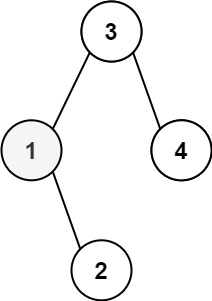
输入：root = [3,1,4,null,2], k = 1
输出：1

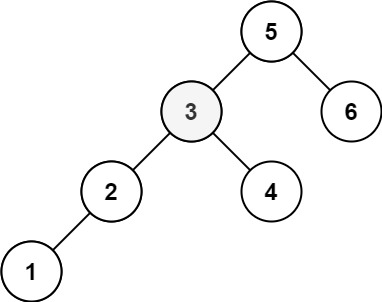
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

限制

• 树中的节点数为 n。
• 1 <= k <= n <= 10^4
• 0 <= Node.val <= 10^4

进阶

• 如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

算法

(中序遍历) $O(n)$

1. 直接按照中序遍历规则遍历整棵二叉搜索树，并用数组记录结点的值。
2. 返回第 k 节点的值。

时间复杂度

• 需要遍历整棵二叉搜索树，故时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储数组。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:

    void solve(TreeNode* cur, vector<int>& vals) {
        if (!cur)
            return;

        solve(cur -> left, vals);
        vals.push_back(cur->val);
        solve(cur->right, vals);
    }

public:
    int kthSmallest(TreeNode* root, int k) {
        vector<int> vals;
        solve(root, vals);

        return vals[k - 1];
    }
};