多重背包-3:单调队列优化

这个知识点看了我一个晚自习,写代码也很犹豫,很多地方不知道怎么写,多少时间对着各位大佬的题解,一个字母一个字母对着敲,对此,我认为有必要用笔记的形式开始整理这个知识点,系统.完整的去了解它

我们先从完全背包优化开始,重新深入多重背包来了解本次的单调队列优化

完全背包优化由来(v代表物品体积,w代表价值):

$f(i,j) = max(f(i-1,j),f(i-1,j-v)+w,f(i-1,j-2*v)+2*w,\dots,f(i-1,j-s*v)+s*w)\\f(i,j-v)=max(f(i-1,j-v),f(i-1,j-2*v)+w,f(i-1,j-3*v)+2*w,\dots,f(i-1,j-s*v)+(s-1)*w)$

我们发现,$f(i,j-v)$代表了$f(i,j)$中从第二个开始后的所有情况,唯一的区别就是少加了一个w,也就是说,如果max的值来自$f(i,j-v)$,就让它加上w就可以了,即 $f(i,j)=max(f(i-1,j),f(i,j-v)+w)$

这里还需要仔细思考一个对我们有利于理解多重背包的点,为什么$f(i,j-v)$的项数相比$f(i,j)$少了一项,原因如下:这里的j-s*v代表是能拿取的最多s件,因为是完全背包,能拿多少取决于你能装多少,你总容量为j,那么最大就能拿到$j-s *v >= 0$的情况,正因为如此,$f(i,j-v)$必然比$f(i,j)$少一项,因为它一开始就比j少了v(即j-v的体积);

好的,我们讲解完了完全背包的优化,同时特别注意了为什么$f(i,j-v)$为什么少了一项,让我们再来观察多重背包(此处只讲单调队列优化,不涉及二进制优化)

依照完全背包再次尝试优化多重背包

$f(i,j) = max(f(i-1,j),f(i-1,j-v)+w,f(i-1,j-2*v)+2*w,\dots,f(i-1,j-s*v)+s*w)\\f(i,j-v)=max(f(i-1,j-v),f(i-1,j-2*v)+w,f(i-1,j-3*v)+2*w,\dots,f(i-1,j-(s+1)*v+s*w)$

居然多了一项,这种情况也不会影响我们继续分析,因为在完全背包那,我们特别注意了s,这里分析分析就能马上明白为什么是(s+1)了,s代表我们最多能拿的,既然我们初始容量变成了j-v,那也能拿s个物品啊,所以就变成了j-(s+1)*v

不能这样优化了,也不必心灰意冷,我们把$f(i,j-v),f(i,j-v),\dots,f(i,r+v),f(i,r)$都分析了(这里的r表示拿了最多的v,直到不能拿v为止了,也就是说$r<v$),就能发现一个有趣的事情:

此处借用大佬的写的latex,图片来源:AcWing 6. 多重背包问题 III【单调队列优化+图示】 - AcWing

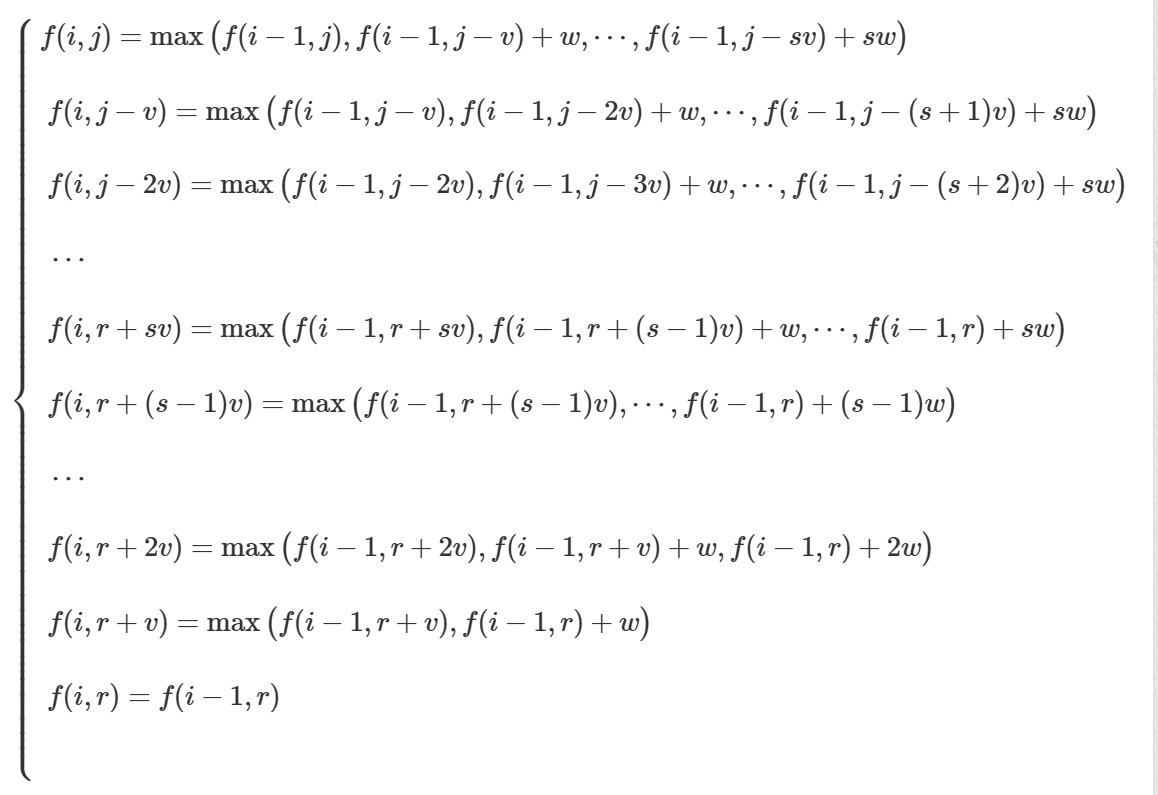
我们从最后往上看,我们发现如下: 第二级和第一级有关,第三级与第一,二都有关,但是需要的w不同,由于每个f都是求max,我们可以想到用一个单调队列来维护最大值,队列大小是s,为啥?因为我们最多只能拿s个物品,观察图片,第一级到s级,项数都是递增的,但是后面最多只能有s级了…不如说,一开始由于空间太少了,所以只能拿那么多,后面空间足够多了,所以能把s拿满.

$f(i,r+v)=max((f(i-1,r+v),f(i,r)+w)),f(i,r+2v)=max(f(i-1,r+2v),f(i+v)+w,\dots,)$

这个式子是我们选择单调队列的关键,虽然是每个式子都是下一级的递推,但是我们一个式子里最多只有s个(即窗口大小),如果窗口没有限制,那么只要记录递推式中的max就可以了,就是因为窗口大小只有s,所以有可能最大值在窗口之前,当弹出窗口后,我们就不知道最大值了,单调队列简直就是为解决这个问题而生的

这里有点难理解,但是我们要注意我们始终的诉求是求max,无论在那个$f$中都是如此,最后一级($f(i,r)$需要加$(j-r)/v$个w),每往上递减一级,就少一个w(想想我们的完全背包,从第二个开始就需要全体加w了,后面的依次都是如此)

至此,写代码的所有条件都满足了,是时候check code了(添加了注释方便理解)

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 20010;

int n, m;
int v[N], w[N], s[N];
int f[M], g[M];//只需要i和i-1层,滚动数组优化
int q[M];//单调队列

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];//体积,价值,最多能拿的数量
    for (int i = 1; i <= n; ++ i)
    {
        //g用于记录i-1层
        memcpy(g, f, sizeof g);
        for (int r = 0; r < v[i]; ++ r)//枚举可能剩余的r
        {
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i])//每次多拿一个
            {
                //判断是否退出队列了
                /* j-q[hh]代表的是当前容量减去队首记录的容量,由于j=r+k*v,k就代表了经过了多少层,由于差距最多为s,所以不能超过s*v
                */
                while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++ ;
                //优先队列,比当前小的都弹出,没用
                //从队首到现在经历了很多级,所以要加上对应个w,再和g[j]比较
                while (hh <= tt && g[q[tt]] + (j - q[tt]) / v[i] * w[i] <= g[j]) -- tt;
                q[ ++ tt] = j;//push当前值
                f[j] = g[q[hh]] + (j - q[hh]) / v[i] * w[i];//赋值
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}