P1135 奇怪的电梯
题目描述
呵呵,有一天我做了一个梦,梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯,而且第 i 层楼(1≤i≤N)上有一个数字 Ki(0≤Ki≤N)。电梯只有四个按钮:开,关,上,下。上下的层数等于当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如: 3,3,1,2,5 代表了 Ki(K1=3,K2=3,……),从 1 楼开始。在 1 楼,按“上”可以到 4 楼,按“下”是不起作用的,因为没有 −2 楼。那么,从 A 楼到 B 楼至少要按几次按钮呢?
输入格式
共二行。
第一行为三个用空格隔开的正整数,表示 N,A,B(1≤N≤200,1≤A,B≤N)。
第二行为 N 个用空格隔开的非负整数,表示 Ki。
输出格式
一行,即最少按键次数,若无法到达,则输出 -1。
输入输出样例 #1
输入 #1
5 1 5
3 3 1 2 5
输出 #1
3
说明/提示
对于 100% 的数据,1≤N≤200,1≤A,B≤N,0≤Ki≤N。
本题共 16 个测试点,前 15 个每个测试点 6 分,最后一个测试点 10 分。
算法1
(dfs) O(n2)
一道搜索题目,写了半天,一直在找漏洞。搞了好久终于弄好了。
通过这题说一些学习dfs的感悟,就是关于回溯,我感觉之前写dfs代码就有st[]数组用来判断是否访问过,其实就是关于回溯的问题,搞的我有点乱,反正用dfs()就会构造搜索树。
像题解里面的代码是这样写的:
void dfs(int node,int step){
dis[node]=step;//一定可以更新
int v=node-k[node];
if(1<=v&&step+1<dis[v]/*可以更新在搜索*/)//下
dfs(v,step+1);
v=node+k[node];
if(v<=n&&step+1<dis[v])//上
dfs(v,step+1);
return;
}
它这样其实也会在搜索树上一步步搜,只是它在搜下一步前进行了剪枝。
还有就是关于回溯里面num的,我感觉也可以写成两种参数的形式代替。
void dfs(int node,int step)
反正多写吧。。感觉懂了又有点乱
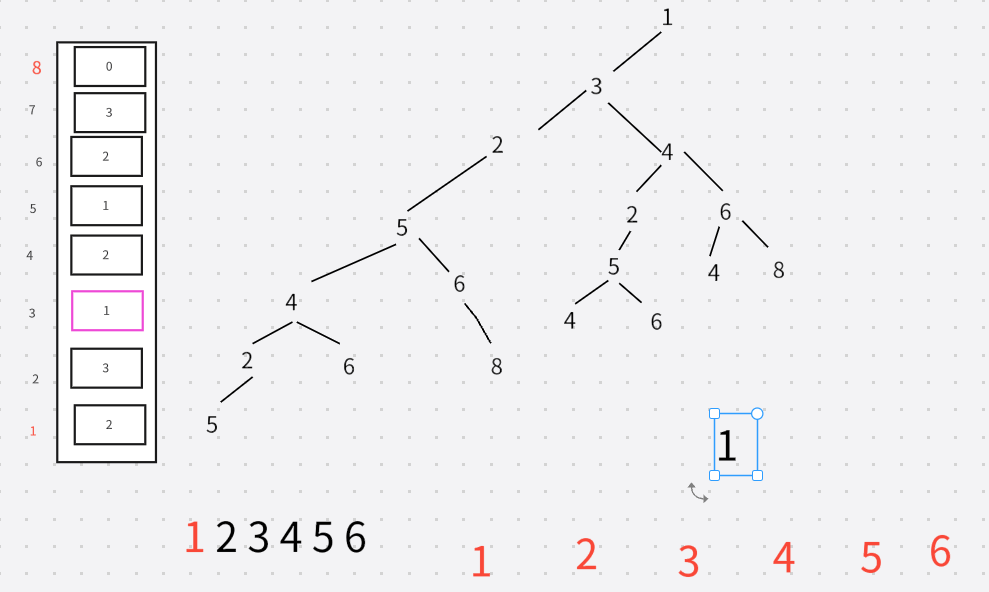
C++ 代码1(数据全过)
这个就是改了很多版的,其中剪枝的步骤很重要,然后相对于代码2,把st[]数组去掉了,我感觉不用也行,它就是一步步搜索的不存在重复访问的问题,因为剪枝的步骤就防止了。
特别注意的是dist[a]=1; 一开始这里设置为一是防止在剪枝的时候特判忽略一种特殊情况:
就是访问又回到起始点a,然后又重新开始搜索,具体改动看代码2。
#include<bits/stdc++.h>
using namespace std;
int arr[251];
int dist[251];//这个数组是用来记录访问的最小次数的
int n,a,b;
int ans=1e9;
int num=0;
void dfs(int la,int fw) //第la层 fw的意思是按钮的次数哈 不是走了多少层
{
if(la==b)
{
ans=min(ans,fw);
return;
}
if(fw>ans) return; //可有可无 有最好
//剪枝
if(fw>=dist[la]) //等于的情况不能剪! wang1:把la写为0
{
return;
}
dist[la]=min(dist[la],fw);
int on,dw;
on=la+arr[la];
dw=la-arr[la];
if(on>=1 && on<=n) dfs(on,fw+1);
if(dw>=1 && dw<=n) dfs(dw,fw+1);
return;
}
int main()
{
memset(dist,0x3f,sizeof (dist));
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>arr[i];
dist[a]=1;
dfs(a,0);
if(ans<1e9) cout<<ans;
else cout<<-1;
return 0;
}
C++ 代码2(数据全过)
这个代码就是没有去除st数组的,很繁琐。
#include<bits/stdc++.h>
using namespace std;
int arr[251];
int dist[251];//这个数组是用来记录访问的最小次数的
int n,a,b;
int ans=1e9;
int num=0;
void dfs(int la,int fw) //第la层 fw的意思是按钮的次数哈 不是走了多少层
{
if(la==b)
{
ans=min(ans,fw);
return;
}
if(fw>=ans) return; //可有可无 有最好
//剪枝
if(fw>dist[la]) //等于的情况不能剪! wang1:把la写为0
{
return;
}
dist[la]=min(dist[la],fw);
int on,dw;
on=la+arr[la];
dw=la-arr[la];
if(on>=1 && on<=n) dfs(on,fw+1);
if(dw>=1 && dw<=n) dfs(dw,fw+1);
return;
}
int main()
{
memset(dist,0x3f,sizeof (dist));
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>arr[i];
dist[a]=1;
dfs(a,0);
if(ans<1e9) cout<<ans;
else cout<<-1;
return 0;
}
C++ 代码3(数据一半超时)
没有剪枝的
#include<bits/stdc++.h>
using namespace std;
int arr[250];
bool st[250];
int n,a,b;
int ans=1e9;
int num=0;
void dfs(int la) //第la层
{
if(la==b)
{
ans=min(ans,num);
return;
}
int on,dw;
on=la+arr[la];
dw=la-arr[la];
if(on>=1 && on<=n)
{
if(!st[on])
{
st[on]=true;
num++;
dfs(on);
num--;
st[on]=false;
}
}
if(dw>=1 && dw<=n)
{
if(!st[dw])
{
st[dw]=true;
num++;
dfs(dw);
num--;
st[dw]=false;
}
}
if((on<1 || on>n) && (dw<1 || dw>n))
{
// ans=-1;
return;
}
else
if(dw<1 && st[on]==true)
{
// ans=-1;
return;
}else
if(on>n && st[dw]==true)
{
return;
}else
if(st[on]==true && st[dw]==true)
{
// ans=-1;
return;
}
}
int main()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>arr[i];
st[a]=true;
dfs(a);
if(ans<1e9) cout<<ans;
else cout<<-1;
return 0;
}

