P1219 [USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 $6 \times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $1\ 2\ 3\ 4\ 5\ 6$

列号 $2\ 4\ 6\ 1\ 3\ 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n \times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例 #1

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于 $100\%$ 的数据，$6 \le n \le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

算法(dfs)

一道很经典的dfs题目。之前做过第二次还是没直接做出来。像这种dfs题目一般有两个搜索变量（自己瞎取的），一个是行 另一个是列，行呢作为搜索的入口 dfs(1)，然后列呢是存在与for()循环中的，就有这种结构

for( )
{
    dfs();
}

然后当行到达某个值的时候，就按照题目要求进行输出或是什么的，一般都是void函数。

本题中的难点在于你的斜对角线只能有一个棋子，用一个数组z[]表示左下到右上的线，f[]反之。
对于z[]你会发现它的行和列的规律是i+j=某个值，对于每条斜线这个值都不重复的。

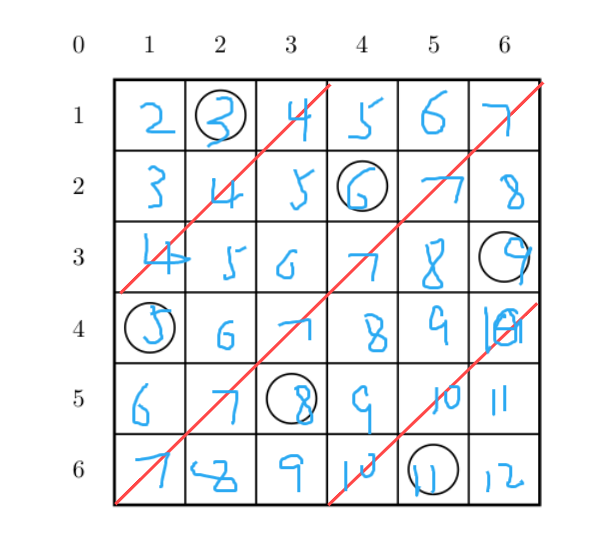
对于f[]呢，你会发现i-j都等于某个值，但是有负数，所以加个n，这样也可以做到是唯一的。

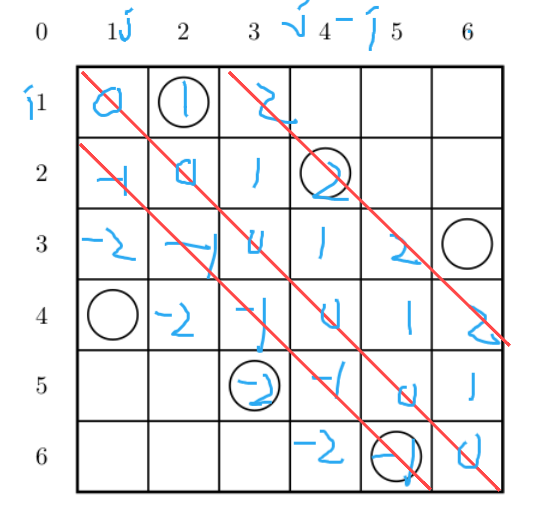
C++ 代码

#include<bits/stdc++.h>
using namespace std;

int n;
int h[100];
bool l[100],z[100],f[100];
int total; 
void dfs(int i)
{
    if(i==n+1)
    {
        total++;
        if(total<=3)
        {
            for(int q=1;q<=n;q++) cout<<h[q]<<' ';
            cout<<endl;
        }
    }
    for(int j=1;j<=n;j++)
    {
        if(!l[j] && !z[i+j] && !f[j-i+n])
        {
            h[i]=j;
            l[j]=true;
            z[i+j]=true;
            f[j-i+n]=true;
            dfs(i+1);
            l[j]=false;
            z[i+j]=false;
            f[j-i+n]=false;
        }

    }
    return ;
}
int main(){
    cin>>n;
    dfs(1);
    cout<<total;

    return 0;
}