AcWing 796. 子矩阵的和【 c++详细题解】

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 796. 子矩阵的和【 c++详细题解】原题链接简单

作者：

林小鹿 , 2020-12-19 20:58:37 , 所有人可见 , 阅读 10954

163

88

二维前缀和推导

如图：

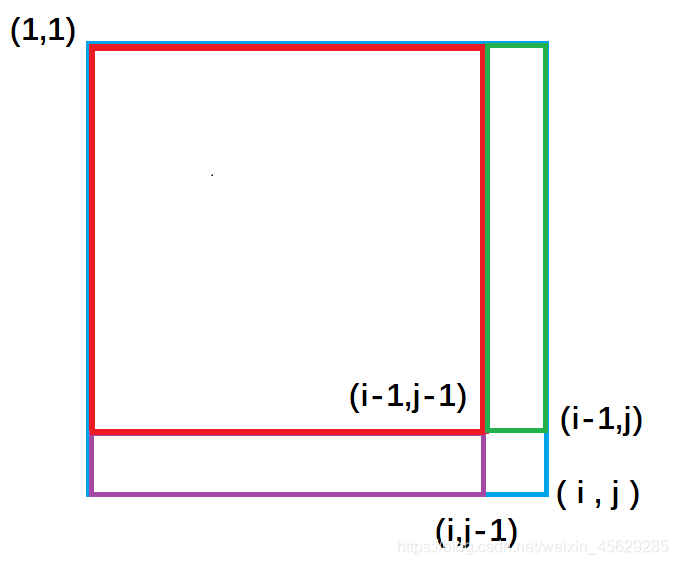{:width=”50%”}

紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。

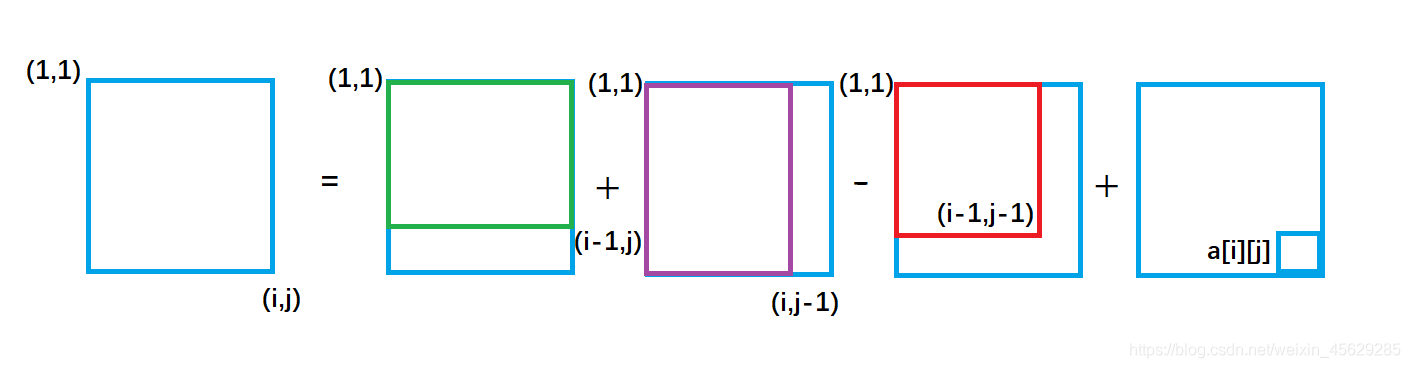
从图中我们很容易看出，整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];

因此得出二维前缀和预处理公式

s[i] [j] = s[i-1][j] + s[i][j-1 ] + a[i] [j] - s[i-1][ j-1]

接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。

如图：
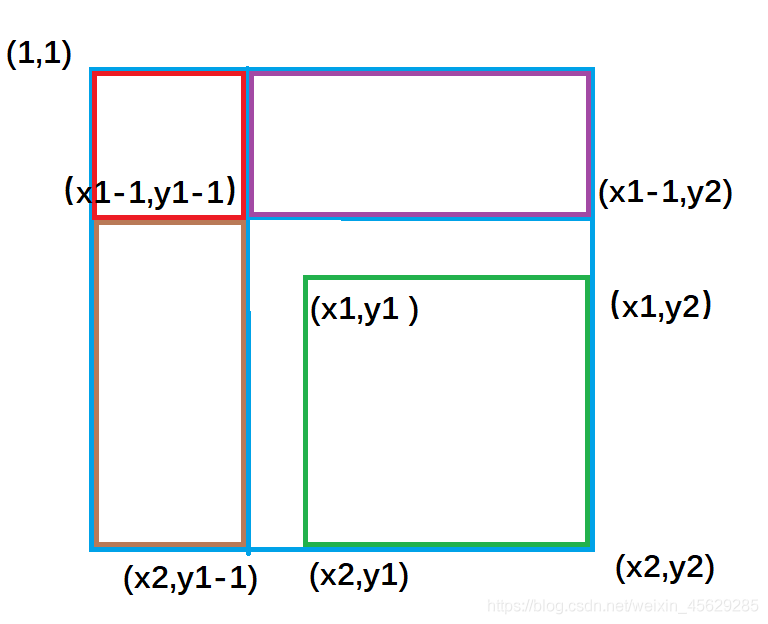{:width=”50%”}

紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积，黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积；

不难推出：

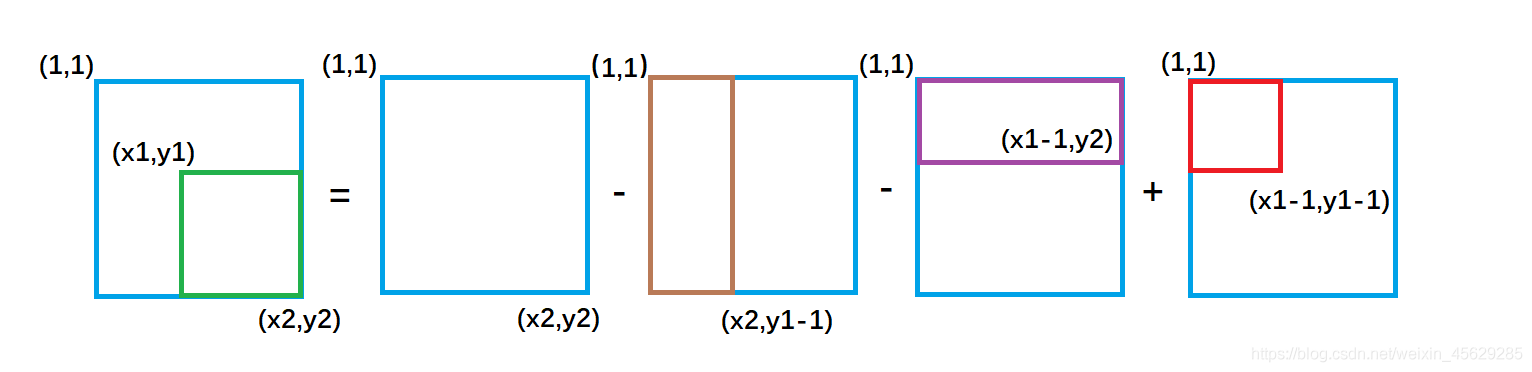
绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]

因此二维前缀和的结论为：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

总结：

代码：

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }

    return 0;
}

44 评论

学不会动态规划不改名 2023-01-08 16:18

博主为什么用cin和cout写会爆栈呢

yago 2023-01-15 13:39

简单来讲scanf 和 cin 在时间效率上差别很大的原因是：
在scanf元素的类型我们已经告知了，机器不用再去查找元素类型，scanf需要自己写格式，是一种格式化输入。
而在cin 元素类型由机器自己查找，cin是字符流输入，需要先存入缓冲区再输入。

xyj23 2022-07-19 20:06

咋还是错的…大佬们帮忙看看啊

#include<iostream>
#include<cstdio>
using namespace std;
int a[1001][1001],x1[200010],y1[200010],x2[200010],y2[200010],d[1001][1001];
int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    for(int i = 0;i < n;i ++){
        for(int j = 0;j < m;j ++){
            cin>>a[i][j];d[i][j]=d[i-1][j]+d[i][j-1]-d[i-1][j-1]+a[i][j];
        }
    }

    for(int i = 0;i < q;i ++)
    {
        cin>>x1[i]>>y1[i]>>x2[i]>>y2[i];
        cout<<d[x2[i]-1][y2[i]-1]+d[x1[i]-2][y1[i]-2]-d[x1[i]-2][y2[i]-1]-d[x2[i]-1][y1[i]-2]<<endl;
    }
    return 0;
}