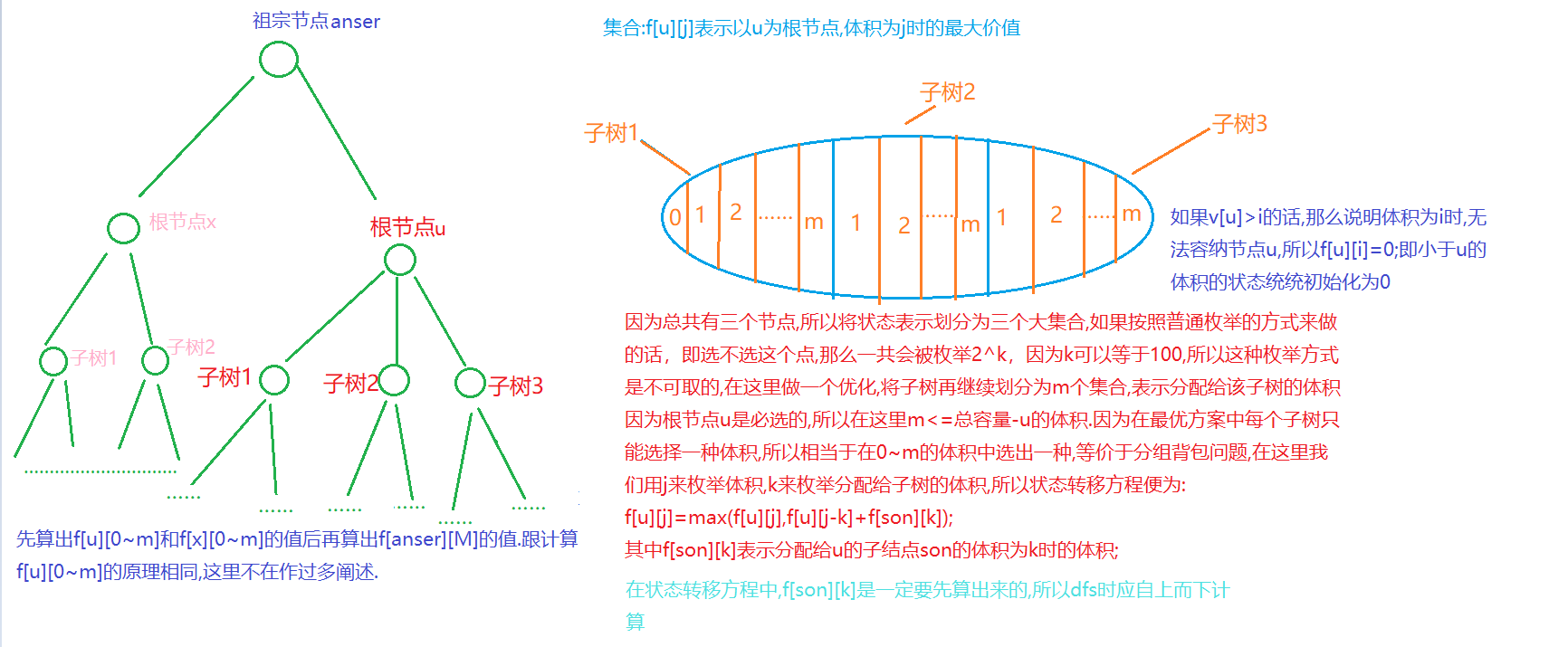
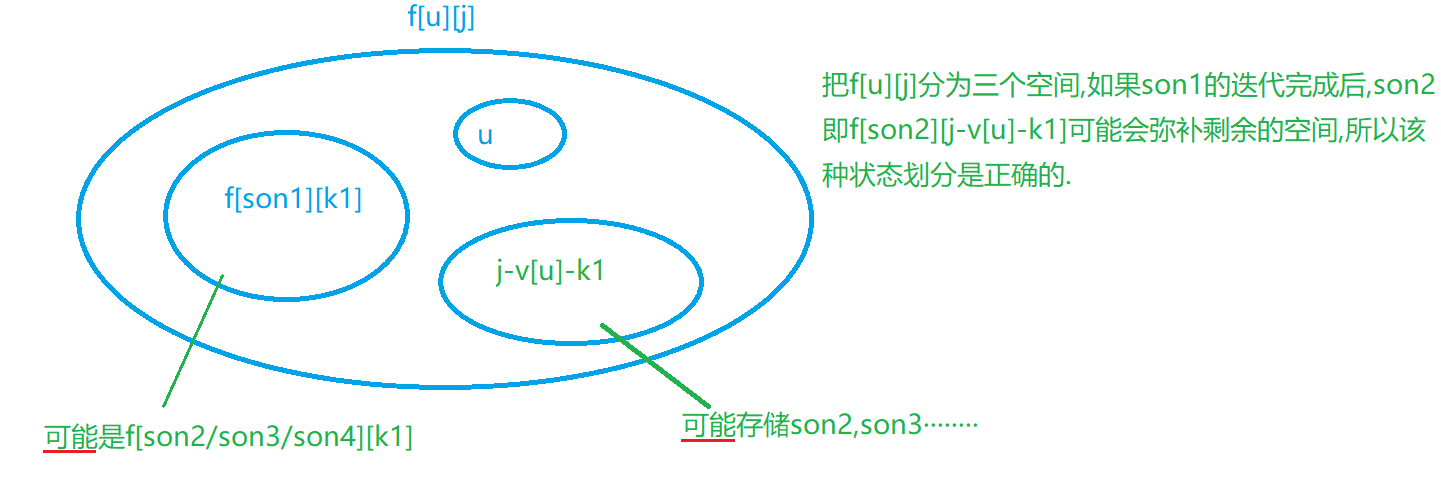
思路

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=110;

int f[N][N],v[N],w[N],h[N],ne[N],e[N],idx;
int n,m;

void add(int a,int b)//a是b的父节点
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u)//因为u是根节点,所以u是必选的
{
    for(int i=h[u];i!=-1;i=ne[i])//枚举子树
    {
        int son=e[i];//记录子树的根节点
        dfs(e[i]);//因为dfs是自下而上的,所以需要从下到上计算

        for(int j=m-v[u];j>=0;j--)//因为u是该树的根节点,所以必选,预留出u的空间
         for(int k=0;k<=j;k++)//枚举该子树分配到的体积
         f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);//加上该子树的值
    }
    //把物品u加进去,因为是根节点
    for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];
    for(int i=0;i<v[u];i++) f[u][i]=0;//如果无法容纳物品u,那他的价值为0;
}

int main()
{
    memset(h,-1,sizeof(h));

    scanf("%d%d",&n,&m);

    int anser;
    for(int i=1;i<=n;i++)
    {
        int p;
        scanf("%d%d%d",&v[i],&w[i],&p);

        if(p==-1) anser=i;//寻找出祖宗节点
        else add(p,i);
    }

    dfs(anser);

    printf("%d",f[anser][m]);

    return 0;
}