常用技巧转换，寻找一个直线旋转

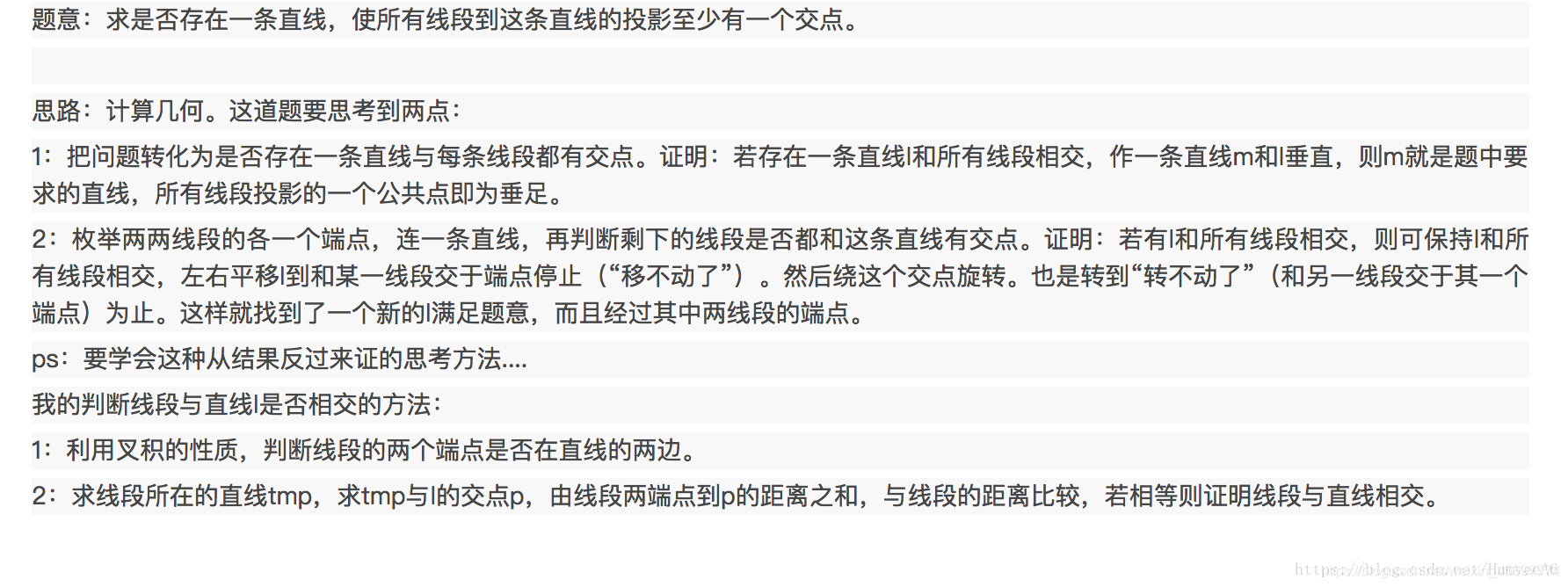
我们发现如果可以找到一个直线与所有的线段都相交，那么我们做一个垂直这个直线的垂线，所有的线段的投影一定都交于这个直线与垂线的垂足处，我们可以很轻松地画图验证这一定理。

所以现在问题就变成了找一个可以穿过所有线段的直线。

我们肯定不能暴力找所有的坐标判断是否相交。

这里我们使用一个计算几何常用的技巧：我们发现所有可能的答案，至少从与一个线段有交点开始。所以我们可以先找一个过一个线段的直线，然后我们旋转他（传统艺能）。我们把这个直线的定点定为这个线段的端点，然后旋转。因为我们要满足能够与其他的线段相交，所以我们旋转的时候有一个限制，就是不能超过另一个线段的一个端点，所以我们可以把所有的候选直线限定到所有线段的端点的连线的直线。

所以我们可以$O(n^2)$，枚举所有线段的端点，然后$O(n)$暴力判断是否都与其他的线段有交点，如果存在一个直线与所有的线段有交点说明一定存在解，输出 Yes!。

那么现在的问题是我们如何判断一个线段和一个直线是否有交点，我们这里只需要判断线段的两个端点是否在直线的异侧即可。

时间复杂度：$O(n^3)$

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <cstring>

using namespace std;
const int N = 50007;
const double eps = 1e-8, DINF = 1e18;
int n, m, t;

struct Point
{
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) { }
};

Point q[N], a[N], b[N];

typedef long long ll;
typedef Point Vector;

Vector operator + (Point A, Point B) {return Vector(A.x + B.x, A.y + B.y);}

Vector operator - (Point A, Point B) {return Vector(A.x - B.x, A.y - B.y);}


int dcmp(double x, double y)
{
    if(fabs(x - y) < eps) return 0;
    if(x < y) return -1; 
    return 1;
}

int sgn(double x)
{
    if(fabs(x) < eps) return 0;
    if(x < 0) return -1;
    return 1;
}

double Dot(Vector A, Vector B) {return A.x * B.x + A.y * B.y;}

double Cross(Vector A, Vector B) {return A.x * B.y - A.y * B.x;}

//A, B:直线上一点,C:待判断关系的点
int relation(Point A, Point B, Point C)
{
    // 1 left -1 right 0 in
    int c = sgn(Cross((B - A), (C - A)));
    if(c < 0) return 1;
    else if(c > 0) return -1;
    return 0;
}

bool check()
{
    for(int i = 0; i < n * 2; ++ i) {
        for(int j = i + 1; j < 2 * n; ++ j) {
            if(!dcmp(q[i].x, q[j].x) && !dcmp(q[i].y, q[j].y)) continue;
            bool flag = true;
            for(int k = 0; k < n; ++ k) {
                if(relation(q[i], q[j], a[k]) * relation(q[i], q[j], b[k]) > 0) {
                    flag = false;
                    break;
                }
            }
            if(flag) return true;
        }
    }
    return false;
}

int main()
{
    scanf("%d", &t);
    while(t -- ) {
        scanf("%d", &n);
        for(int i = 0, k = 0; i < n; ++ i) {
            double x1, x2, y1, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            q[k ++ ] = {x1, y1}, q[k ++ ] = {x2, y2};
            a[i] = {x1, y1}, b[i] = {x2, y2};
        }

        if(check()) puts("Yes!");
        else puts("No!");
    }
    return 0;
}