AcWing 797. 差分【c++详细题解】

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 797. 差分【c++详细题解】原题链接简单

作者：

林小鹿 , 2020-12-18 16:20:00 , 所有人可见 , 阅读 35989

878

521

差分

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

差分数组：

首先给定一个原数组a：a[1], a[2], a[3],,,,,, a[n];

然后我们构造一个数组b ： b[1] ,b[2] , b[3],,,,,, b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

考虑如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

........

b[n] = a[n] - a[n-1];

图示:

我们只要有b数组，通过前缀和运算，就可以在O(n) 的时间内得到a数组。

知道了差分数组有什么用呢？ 别着急，慢慢往下看。

话说有这么一个问题：

给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c;

暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法。

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。

首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;

然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;

为啥还要打个补丁？

我们画个图理解一下这个公式的由来:

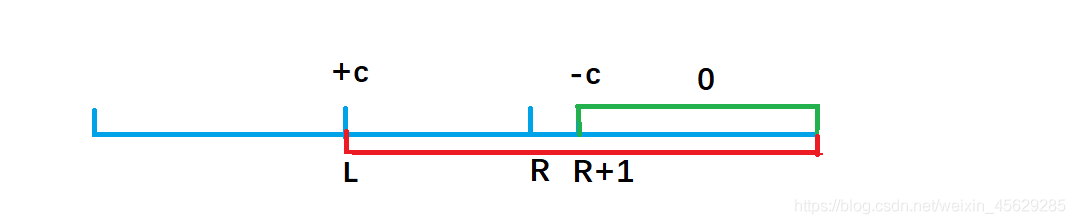
b[l] + c，效果使得a数组中 a[l]及以后的数都加上了c(红色部分)，但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

因此我们得出一维差分结论：给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。

总结：

AC代码

//差分 时间复杂度 o(m)
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];      //构建差分数组
    }
    int l, r, c;
    while (m--)
    {
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;     //将序列中[l, r]之间的每个数都加上c
        b[r + 1] -= c;
    }
    for (int i = 1; i <= n; i++)
    {
        a[i] = b[i] + a[i - 1];    //前缀和运算
        printf("%d ", a[i]);
    }
    return 0;
}

168 评论

Kaisa 2022-09-24 22:32

感谢，比y总的容易理解（对于新手）

i吃橘子 2022-10-30 13:01

雀氏

山川故里 2023-01-04 14:43

同感

怎得 2023-02-03 00:28

是这样的

原神怎么了你 2023-02-19 15:15

比y总讲的好，一看就理解了

云与月 2023-04-01 16:31

同感

Love_cheng 11个月前回复了云与月的评论

太有实力啦

有空我就学算法 8个月前

借楼
n,p = map(int,input().split())
q = list(map(int,input().split()))
b = [0]*(n+2)
def insert(l,r,c):
global b
b[l] = b[l] +c
b[r+1] = b[r+1] - c
for i in range(n):
q[i] = int(q[i])
insert(i+1,i+1,q[i])
for i in range(p):
l,r,c = map(int,input().split())
insert(l,r,c)
cnt = 0
min1 = 101
for i in range(1,n+1):
cnt = cnt + b[i]
if cnt<min1:
min1 = cnt
print(min1)
洛谷上的题同差分数据为6e6，爆内存，c++可以但是python不行，我该怎么优化，求大佬帮忙

不与世俗纷争 3个月前

确实比y总的容易理解一些

Obscure 2021-11-08 21:00

随便记录点，希望对看不懂的有帮助

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];      //构建差分数组
    }
    //上面是构建差分数组，
    // b[1]=a[1]-a[0]
    // b[2]=a[2]-a[1]
    // b[3]=a[3]-a[2]
    // ·········
    // b[6]=a[6]-a[5];
    //目的是为了在前缀和中通过b里的某个元素修改后去修改a后面的值
    //构造了差分数组后就已经有了比如a[3]=b[3]+b[2]+b[1];这种前缀和关系。
    //只不过现在不用，因为为了去修改a的值我们还需要对中间的b进行修改，所以接下来
    //是先对b修改，再调用a[3]=b[3]+b[2]+b[1];
    int l, r, c;
    while (m--)
    {
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;     //将序列中[l, r]之间的每个数都加上c
        b[r + 1] -= c;
    }


    //调用a[3]=b[3]+b[2]+b[1];这种前缀和运算。
    for (int i = 1; i <= n; i++)
    {
        a[i] = b[i] + a[i - 1];    //前缀和运算
        printf("%d ", a[i]);
    }
    //前缀和运算a[3]=b[3]+b[2]+b[1] 因为前面已经构造了差分数组所以此时一定是成立的 //而且如果 中间的某个b不变的话那么a 就不会变。
    // a[3]=b[3]+b[2]+b[1] 
    //a[4]=b[4]+b[3]+b[2]+b[1]
    //他们可以直接写成这个样子
    //那么对中间的b[3] 修改了就是对a[3] 之后的值都修改了
    //这种。
    return 0;
}

西皮皮膏体儿 2022-02-09 11:04

豁然开朗

cjjj 2023-07-10 20:58

大佬好厉害，想问一下 a[N]写成全局变量，是因为会自动初始化为0 就不用初始化a[0]为0了嘛

Louis_You 2023-07-17 16:38 回复了 cjjj 的评论

额

一般信竞选手都会把大部分数组设为全局定义

不过，你说得对。

cjjj 12个月前回复了 Louis_You 的评论

谢谢大佬～

bryant_Lin 2022-07-11 13:57

简化了一下代码，减少了一个数组

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r+1] -= c;
}

int main()
{
    cin >> n >> m;
    for(int i=1; i<=n; i++)
    {
        int x;
        cin >> x;
        insert(i, i, x);
    }

    while(m--)
    {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l, r, c);
    }

    for(int i=1; i<=n; i++)
    {
        b[i] = b[i-1] + b[i];
        cout << b[i] << " ";
    }

    return 0;
}

羊村村花 2023-01-16 12:23

差分跟多米诺骨牌一样，前一个和跟后一个有联系才能一个一个接着往前推

5716 2022-05-05 12:23

笨死了 2023-03-20 12:36

学习总结了一、二维前缀和差分，希望对你有帮助~
https://blog.csdn.net/m0_74215326/article/details/129620912?spm=1001.2014.3001.5502

awhiteboy 2023-03-27 21:50

tql

Tomorrowland. 7天前

说实话，y总确实讲课水平不怎么样，评论区的大佬还是牛的

不与世俗纷争 3个月前

 /*
            假设一开始所有原数组全为0，则差分数组也全部为0
            读取的每一个a[i](就是相当于在原数组的区间[i,i]的数都加上了一个a[i])
            就相当于是在差分数组中对应的b[i]位置上加上a[i],b[i+1]的位置上减去了a[i]
        */

崔秀彬匿名女友 4个月前

谢谢太牛了！

hfuu1 5个月前

感谢感谢

伯纳多 8个月前

这下通透了！！！

秋刀鱼_6 2023-05-09 16:24

a[i] = b[i] + a[i - 1]; //前缀和运算
假设L=1,r=10
看不懂这一步的：
i=1时 a[1]=b[1]+a[0]=a[1]+c
i=2时 a[2]=b[2]+a[1]=(a[2]-a[1])+a[1]+c=a[2]+c

Pobz 2023-01-06 08:54

羊村村花 2023-01-16 12:25

老哥怎么发图片的

羊村村花 2023-01-16 12:27 回复了羊村村花的评论

懂了哈哈

![1](https://bqb12.bingping.top/Uploads/vod/2018-08-07/5b6870eb6d191.jpg)

Pobz 2023-01-16 12:31 回复了羊村村花的评论

$\color{Magenta}{hhh,我也才学的makedown语言}$

salary 2023-02-13 22:11 回复了羊村村花的评论

原神怎么了你 2023-02-19 15:17 回复了 salary 的评论

pdsujc06 6个月前回复了羊村村花的评论

#好高级
太酷了

这是什么

pdsujc06 6个月前回复了 pdsujc06 的评论

Javaer 2022-12-18 01:35

感谢林子哥解决了我2h的困扰

懒惰的蚩蚩 2022-07-21 09:46

题解写得真好！！

FXW 2022-06-16 09:20

大佬，你给的代码运行后输出的结果中最后一位数与标准答案不一样呢，

evil_7 2022-05-15 09:36

大佬在人间

Newoahil 2022-04-27 18:35

Orz

DongTang 2022-04-22 01:22

提醒一下，如果开辟的是大小为n + 1的动态数组的话，在
while (m–)
{
scanf(“%d%d%d”, &l, &r, &c);
b[l] += c; //将序列中[l, r]之间的每个数都加上c
b[r + 1] -= c;
}
这里面，要对b[r + 1] -= c;进行判断if(r < n)，否则会出现数组越界

湘圆琴子- 2021-10-10 18:03

太赞了。y总第第二个for循环我硬是没看懂啥意思，你的代码我看下就理解了！！！！

AcWing 797. 差分 【c++详细题解】 原题链接 简单

差分

168 评论

AcWing 797. 差分【c++详细题解】原题链接简单