算法思路

传统dp背包问题的做法是这样的:

 for(int i=1;i<=n;i++) 
  for(int j=0;j<=m;j++)
   for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
    f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);

即枚举到第i个物品时,要将f[0~m]的状态全部都更新一遍.
状态转移方程为:
f[i][j]=max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2v]+2w,……,f[i-1][j-sv]+sw);
这样的时间复杂度过大,而且
f[i][j]=max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2v]+2w,……,f[i-1][j-sv]+sw);
f[i][j-v]+w=max(      f[i-1][j-v]+w,f[i-1][j-2v]+2w,……,f[i-1][j-sv]+sw,f[i-1][j-(s+1)]+(s+1)w);
所以无法像完全背包一样进行优化,所以在这里我们换一个思路

因为每次循环都只需要用到第i-1层的结果,所以在这里:
f:第i层结果
g:第i-1层结果

因为枚举到第i个物品时,要将f[0~m]的状态全部都更新一遍.所以在这里
f[j]为体积为j的情况下获得价值的最大值,对于每一个物品i来说都要更新f[0]~f[m]的值,枚举完i个物品之后,f[m]就是最优解.
讲到这里先举个例子,0~11可以如何表示出来呢?答:
0 3 6 9 
1 4 7 10
2 5 8 11
所以f[0]~f[m]的状态也可以这样表示出来:
f[0], f[v],   f[2*v],   f[3*v],   …… , f[k*v]
f[1], f[v+1], f[2*v+1], f[3*v+1], …… , f[k*v+1]
f[2], f[v+2], f[2*v+2], f[3*v+2], …… , f[k*v+2]
...
f[r], f[v+r], f[2*v+r], f[3*v+r], …… , f[k*v+r]
其中0<r<v,如果有f[x]中,x>m的,会在代码中被筛除,其中m=k*v+x;(0<x<=r);

所以f[0]~f[m]就被划分成了r个部分;
那么f[j]该如何表示呢?

如果一共有3个物品,即s=3的话:
那么f[3*v+1]的最大值为
f[3*v+1]=max(g[3*v+1],g[2*v+1]+w,g[v+1]+2w,g[1]+3w);
所以我们可以得到下列算式:(其中r表示余数)
f[r]=      g[r];
f[r+v]= max(g[r]+w,g[r+v]);
f[r+2v]=max(g[r]+2w,g[r+v]+w, g[r+2v],);
f[r+3v]=max(g[r]+3w,g[r+v]+2w,g[r+2v]+w,g[r+3v]);
……
f[r+sv]=max(g[r]+sw,……,g[r+(s-1)v]+w,g[r+sv]);
可以发现上面的等式上下存在偏移量w,所以可以减去kw再加上kw进行转换
f[r]= g[r];
f[r+v]= max(g[r],g[r+v]-w)+w;
f[r+2v]=max(g[r],g[r+v]-w,g[r+2v]-2w)+2w;
f[r+3v]=max(g[r],g[r+v]-w,g[r+2v]-2w,g[r+3v]-3w)+3w;
……
f[r+sv]=max(g[r],……,g[r+(s-1)v]-(s-1)w,g[r+sv]-sw)+sw;

等式化简完后我们在来看看所需要的数据结构:

本题所需的数据结构为单调队列,如果遗忘可以参考:

https://www.acwing.com/activity/content/code/content/399412/

可以由上方的推导的公式可以知道每次入队时的数为:
q[tt]=r+k*v,对应在g数组中的值为:g[r+k*v]-k*w;(k表示物品数量)
单调队列中对比队尾大小时应对比q[tt]所对应g数组中的值;
所以比较的代码为:
while(hh<=tt&&g[r+k1*v]-(r+k1*v-r)/v*w<=g[r+k*v]-(r+k*v-r)/v*w) --tt;
即:
while(hh<=tt&&g[q[tt]]-(q[tt]-r)/v*w<=g[j]-(j-r)/v*w) --tt;
如果总共有3件物品的话:

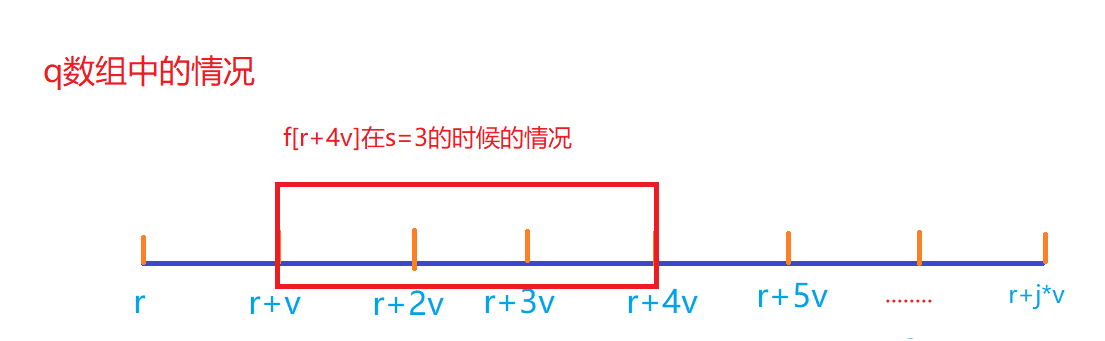
所以在q数组中需要保证长度为s.因为每次队首都是最大值,所以状态转移方程为:
f[j]=g[q[hh]]+(j-q[hh])/v*w;

无注解版代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=20099;

int f[N],g[N],q[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++)
    {
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);

        memcpy(g,f,sizeof(f));
        for(int r=0;r<v;r++)
        {
            int tt=-1,hh=0;
            for(int j=r;j<=m;j+=v)
            {
                while(hh<=tt&&q[hh]<j-s*v) ++hh;
                while(hh<=tt&&g[q[tt]]-(q[tt]-r)/v*w<=g[j]-(j-r)/v*w) --tt;
                q[++tt]=j;
                f[j]=g[q[hh]]+(j-q[hh])/v*w;
            }
        }
    }

    cout<<f[m]<<endl;

    return 0;

}

注解版代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=20099;

int f[N],g[N],q[N];
//f存储的是第i层,g存储第i-1层,q存储的是f,g数组中的下标(体积,例如:q[5]=r+3v);

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++)
    {
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);

        memcpy(g,f,sizeof(f));//复制上一层的结果
        for(int r=0;r<v;r++)//枚举余数
        {
            int tt=-1,hh=0;//tt代表队尾,hh代表对头(最前面的元素)
            for(int j=r;j<=m;j+=v)//枚举体积,单调队列模板
            {
                while(hh<=tt&&q[hh]<j-s*v) ++hh;//判断是否超出了s件物品;
                /*
                如果q[hh]恰好等于r的话,j=s*v+r时,j-s*v=r,此时正好有s个物品
                q[hh]=j-s*v,如果有s+1个物品时,j=(s+1)*v+r-s*v=r+v,大于r,就
                超过了物品范围范围;r+2v同理,如果j=(s+2)+r是则正好有s件物品
                通过等式,如果j=(s+3)v+r则有s+1间物品,无法通过等式.
                */
                while(hh<=tt&&g[q[tt]]-(q[tt]-r)/v*w<=g[j]-(j-r)/v*w) --tt;
                //将前面推导出来的公式进行比较
                q[++tt]=j;
                /*
                因为f[j]=max(g[j],g[j-v]+w,····)其中g[j]也是需要参与的,所以更新应放在
                前面,否则如果g[j]恰好是最大的的方案,那么会导致结果的错误;
                */
                f[j]=g[q[hh]]+(j-q[hh])/v*w;//更新最大的值
            }
        }
    }

    cout<<f[m]<<endl;//输出最终结果

    return 0;

}
如果有问题欢迎提出