更好的阅读体验

Statement

给定一个长为 $n$ 的数组 $d$ ，每次可以选择一段连续区间 $[L,R]$ 并全部加一。问最少几次能将整个数组变成 $0$ .

$1\leq n\leq 1e5,0\leq d_i\leq 1e4$

Thoughts & Solution

一个很显然的想法是，如下图将所有的凹陷部分以尽可能连续的横向方块填充：（数据为样例）

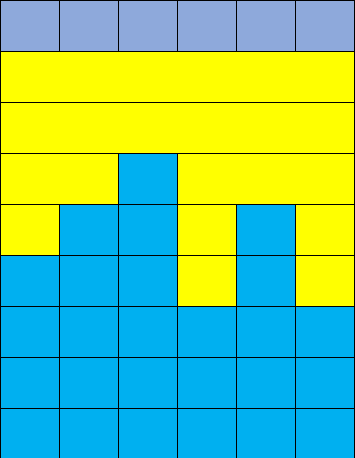
（图中最上面一行为地面，黄色部分每一块就是一次填充）很显然这样就是最优方案。

实现也很简单：从右往左遍历，如果当前 $a[i]$$<$$a[i-1]$ ，就相当于结束掉了上一个横条，不用动；如果当前 $a[i]>a[i-1]$ ，说明又要新建 $a[i]-a[i-1]$ 个横条，计入答案即可。

复杂度 $\mathcal{O}(n)$ .

//Author: RingweEH
int n,las,ans;

int main()
{
    n=read(); las=ans=0;
    for ( int i=1,x; i<=n; i++ )
    {
        x=read();
        if ( x>las ) ans+=(x-las);
        las=x;
    }

    printf( "%d\n",ans );

    return 0;
}