事件发生的期望的线性性$E(aX+bY) = aE(X)+bE(Y) = p(X) \times E(X)+p(Y) \times E(Y)$
将问题转为图
起点->终点的路径的期望长度
点(状态) 边(状态转移)
$f[a][b][c][d][x][y]:从当前状态跳到终点的期望长度$
$a张黑桃,b张红桃,c张梅花,d张方块$
$大王状态x,小王状态y:0 \sim 3表示放到abcd4堆中,4表示没有被翻出来$
则我们只需分析$f[a][b][c][d][x][y]$能够转移成哪些状态,期望就能用线性公式转移得到

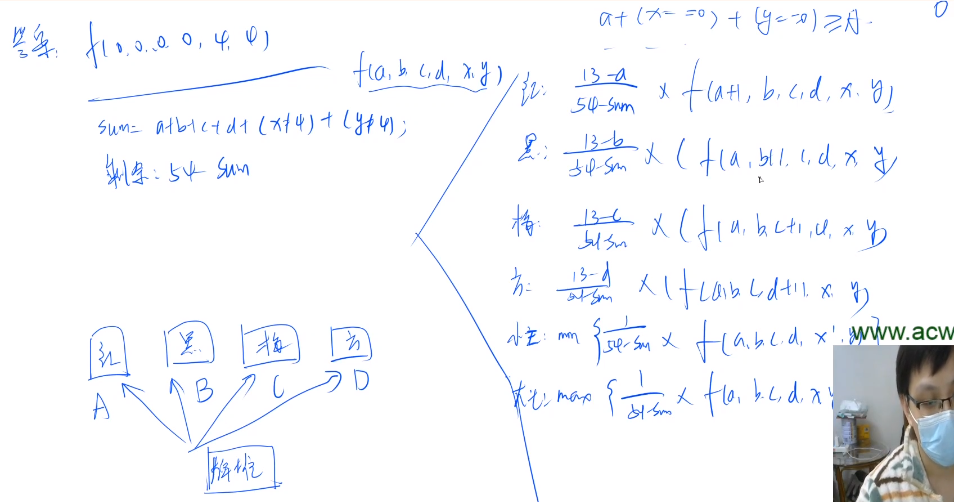
小王大王转移:(目标是使$E$尽可能小,所以取最小的一个方案去替换4种牌中的哪个)
$$ min_{i=0}^{3} \frac{1}{sum} f[a][b][c][d][i][y] + min_{j=0}^{3} \frac{1}{sum} f[a][b][c][d][x][j] $$

$why每个节点v初始化v=1?$
by王道烩dl

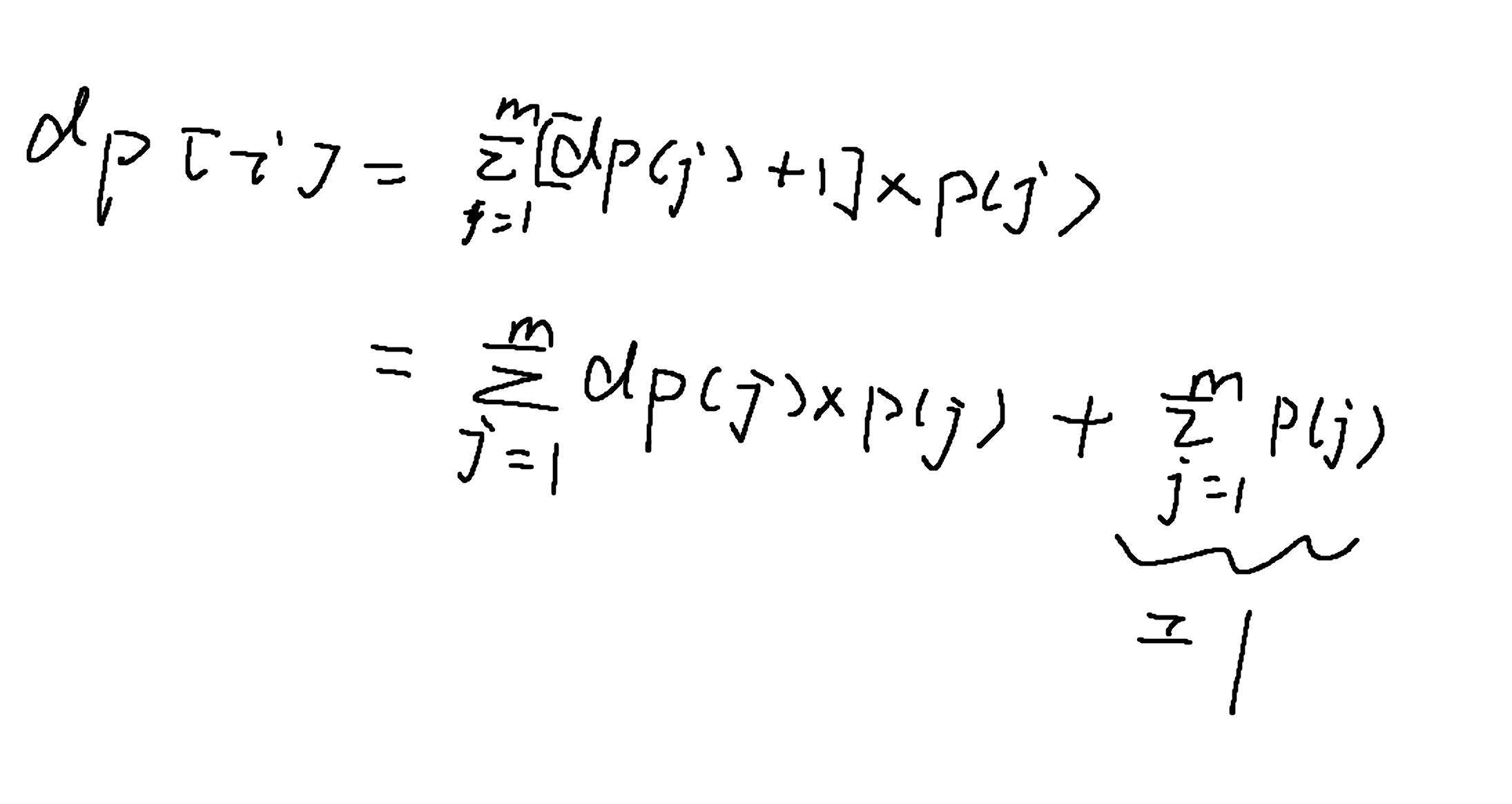
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 14;
const double INF = 1e20;

int A, B, C, D;
double f[N][N][N][N][5][5];

double dp(int a,int b,int c,int d,int x,int y)
{
    double &v = f[a][b][c][d][x][y];
    if (v >= 0) return v;
    // 4个牌堆有的数量
    int as = a + (x == 0) + (y == 0);
    int bs = b + (x == 1) + (y == 1);
    int cs = c + (x == 2) + (y == 2);
    int ds = d + (x == 3) + (y == 3);

    if (as >= A && bs >= B && cs >= C && ds >= D) return v = 0;
    // 目前四个牌堆已经共有sum个
    int sum = a + b + c + d + (x != 4) + (y != 4);
    // 总剩余
    sum = 54 - sum;
    if (sum <= 0) return v = INF;
    // 四种花色
    v = 1;//到下一层的各个节点的期望的和 Σp(j) for j in ne[i]
    if (a < 13) v += (13.0 - a) / sum * dp(a + 1, b, c, d, x, y);
    if (b < 13) v += (13.0 - b) / sum * dp(a, b + 1, c, d, x, y);
    if (c < 13) v += (13.0 - c) / sum * dp(a, b, c + 1, d, x, y);
    if (d < 13) v += (13.0 - d) / sum * dp(a, b, c, d + 1, x, y);
    // 小王
    if (x == 4)
    {
        double t = INF;
        for (int i = 0; i < 4; i ++ ) t = min(t, 1.0 / sum * dp(a, b, c, d, i, y));
        v += t;
    }
    // 大王
    if (y == 4)
    {
        double t = INF;
        for (int i = 0; i < 4; i ++ ) t = min(t, 1.0 / sum * dp(a, b, c, d, x, i));
        v += t;
    }

    return v;
}

int main()
{
    cin >> A >> B >> C >> D;
    memset(f, -1, sizeof f);

    double t = dp(0, 0, 0, 0, 4, 4);
    if (t > INF / 2) t = -1;

    printf("%.3lf\n", t);

    return 0;
}