题目描述

有两棵 无向 树，分别有 n 和 m 个树节点。两棵树中的节点编号分别为 [0, n - 1] 和 [0, m - 1] 中的整数。

给你两个二维整数 edges1 和 edges2，长度分别为 n - 1 和 m - 1，其中 edges1[i] = [a_i, b_i] 表示第一棵树中节点 a_i 和 b_i 之间有一条边，edges2[i] = [u_i, v_i] 表示第二棵树中节点 u_i 和 v_i 之间有一条边。同时给你一个整数 k。

如果节点 u 和节点 v 之间路径的边数小于等于 k，那么我们称节点 u 是节点 v 的 目标节点。注意 ，一个节点一定是它自己的 目标节点。

请你返回一个长度为 n 的整数数组 answer，answer[i] 表示将第一棵树中的一个节点与第二棵树中的一个节点连接一条边后，第一棵树中节点 i 的 目标节点 数目的 最大值。

注意，每个查询相互独立。意味着进行下一次查询之前，你需要先把刚添加的边给删掉。

样例

输入：
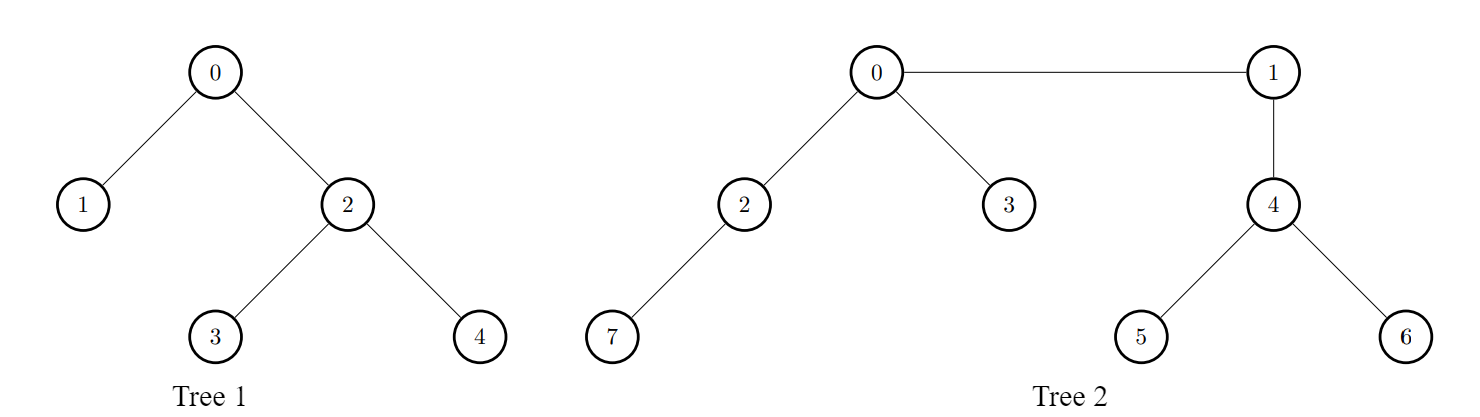
edges1 = [[0,1],[0,2],[2,3],[2,4]]
edges2 = [[0,1],[0,2],[0,3],[2,7],[1,4],[4,5],[4,6]]
k = 2

输出：[9,7,9,8,8]

解释：

对于 i = 0，连接第一棵树中的节点 0 和第二棵树中的节点 0。
对于 i = 1，连接第一棵树中的节点 1 和第二棵树中的节点 0。
对于 i = 2，连接第一棵树中的节点 2 和第二棵树中的节点 4。
对于 i = 3，连接第一棵树中的节点 3 和第二棵树中的节点 4。
对于 i = 4，连接第一棵树中的节点 4 和第二棵树中的节点 4。

输入：
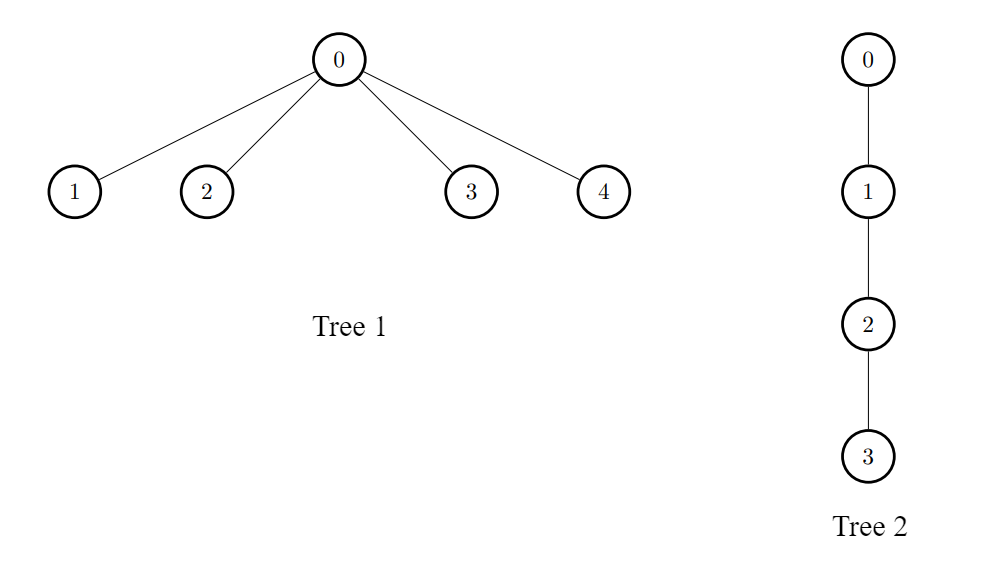
edges1 = [[0,1],[0,2],[0,3],[0,4]]
edges2 = [[0,1],[1,2],[2,3]]
k = 1

输出：[6,3,3,3,3]

解释：

对于每个 i，连接第一棵树中的节点 i 和第二棵树中的任意一个节点。

限制

• 2 <= n, m <= 1000
• edges1.length == n - 1
• edges2.length == m - 1
• edges1[i].length == edges2[i].length == 2
• edges1[i] = [a_i, b_i]
• 0 <= a_i, b_i < n
• edges2[i] = [u_i, v_i]
• 0 <= u_i, v_i < m
• 输入保证 edges1 和 edges2 都表示合法的树。
• 0 <= k <= 1000

算法

(思维题，暴力枚举，宽度优先遍历) $O(n^2 + m^2)$

1. 注意到，对于每个查询第一棵树的节点 $i$，新增的边一定是从节点 $i$ 出发，到第二棵树的固定节点 $u$。
2. 其中，固定节点 $u$ 需要满足拥有最多的 $k-1$ 条边可达的节点数量。
3. 可以通过暴力枚举和宽度优先遍历找到节点 $u$。
4. 然后对于第一棵树的每个节点，同样进行宽度优先遍历，求出最多有多少个节点 $k$ 条边可达。两者相加就能得到答案。

时间复杂度

• 两棵树每个节点进行一次宽度优先遍历，故总时间复杂度为 $O(n^2 + m^2)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储宽度优先遍历的队列和距离数组。

C++ 代码

const int N = 1010;

class Solution {
private:
    queue<int> q;
    int d[N];

    int bfs(int st, const vector<vector<int>> &graph, int k) {
        if (k < 0)
            return 0;

        const int n = graph.size();
        for (int i = 0; i < n; i++)
            d[i] = INT_MAX;

        int cnt = 0;
        q.push(st);
        d[st] = 0;

        while (!q.empty()) {
            int u = q.front();
            q.pop();
            ++cnt;

            for (int v : graph[u]) {
                int nd = d[u] + 1;
                if (d[v] > nd && nd <= k) {
                    d[v] = nd;
                    q.push(v);
                }
            }
        }

        return cnt;
    }

public:
    vector<int> maxTargetNodes(vector<vector<int>>& edges1,
        vector<vector<int>>& edges2, int k
    ) {
        const int n1 = edges1.size() + 1;
        const int n2 = edges2.size() + 1;

        vector<vector<int>> graph1(n1);
        vector<vector<int>> graph2(n2);

        for (const auto &e : edges1) {
            graph1[e[0]].push_back(e[1]);
            graph1[e[1]].push_back(e[0]);
        }

        for (const auto &e : edges2) {
            graph2[e[0]].push_back(e[1]);
            graph2[e[1]].push_back(e[0]);
        }

        int ma = 0;
        for (int i = 0; i < n2; i++)
            ma = max(ma, bfs(i, graph2, k - 1));

        vector<int> ans(n1);
        for (int i = 0; i < n1; i++)
            ans[i] = bfs(i, graph1, k) + ma;

        return ans;
    }
};