题目描述

存在一棵具有 n 个节点的无向树，节点编号为 0 到 n - 1。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [u_i, v_i, w_i] 表示在树中节点 u_i 和 v_i 之间有一条权重为 w_i 的边。

你的任务是移除零条或多条边，使得：

• 每个节点与至多 k 个其他节点有边直接相连，其中 k 是给定的输入。
• 剩余边的权重之和 最大化。

返回在进行必要的移除后，剩余边的权重的 最大 可能和。

样例

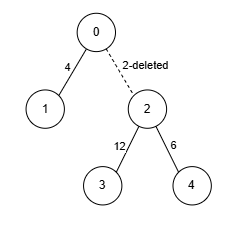
输入： edges = [[0,1,4],[0,2,2],[2,3,12],[2,4,6]], k = 2

输出： 22

解释：

节点 2 与其他 3 个节点相连。我们移除边 [0, 2, 2]，确保没有节点与超过 k = 2 个节点相连。
权重之和为 22，无法获得更大的和。因此，答案是 22。

输入： edges = [[0,1,5],[1,2,10],[0,3,15],[3,4,20],[3,5,5],[0,6,10]], k = 3

输出： 65

解释：

由于没有节点与超过 k = 3 个节点相连，我们不移除任何边。
权重之和为 65。因此，答案是 65。

限制

• 2 <= n <= 10^5
• 1 <= k <= n - 1
• edges.length == n - 1
• edges[i].length == 3
• 0 <= edges[i][0] <= n - 1
• 0 <= edges[i][1] <= n - 1
• 1 <= edges[i][2] <= 10^6
• 输入保证 edges 形成一棵有效的树。

算法

(树形动态规划) $O(n \log n)$

1. 设状态 $f(u)$ 表示以 $u$ 为根的子树满足题目条件，且 $u$ 不与父节点发生连接的最大权重。$g(u)$ 表示以 $u$ 为根的子树满足题目条件，且 $u$ 可以与父节点发生连接的最大权重。
2. 将无根树视为有根树，从 $0$ 开始进行树形动态规划。
3. 每次先递归所有子节点，然后求解当前节点的 $f$ 和 $g$ 值。
4. 求解时，先求出子节点 $f$ 值之和，作为当前节点 $f$ 和 $g$ 的初始值。然后，将每个子节点的 $g$ 值加上边的权重，再与 $f$ 值之差存储一个数组中待定。如果这个差值大于 0，说明选中这条边的收益是更大的，否则就无收益，所以可以只存大于 0 的子节点的差值。
5. 排序差值数组，选出前 $k$ 和 $k - 1$ 大的差值，分别累加到 $f$ 和 $g$ 上。
6. 最终答案为 $f(0)$。

时间复杂度

• 每一层递归需要遍历并排序，故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储邻接表，动态规划的状态，临时数组和递归的系统栈。

C++ 代码

#define LL long long

class Solution {
private:
    vector<vector<pair<int, int>>> graph;
    vector<LL> f, g;

    void solve(int u, int fa, int k) {
        LL b = 0;
        vector<LL> d;

        for (const auto &p : graph[u]) {
            if (p.first == fa)
                continue;

            solve(p.first, u, k);

            b += f[p.first];
            LL t = g[p.first] + p.second - f[p.first];
            if (t > 0)
                d.push_back(t);
        }

        sort(d.begin(), d.end(), [](LL x, LL y) {
            return x > y;
        });

        const int m = d.size();

        for (int i = 0; i < min(k - 1, m); i++)
            b += d[i];

        f[u] = g[u] = b;
        if (m >= k)
            f[u] += d[k - 1];   
    }

public:
    LL maximizeSumOfWeights(vector<vector<int>>& edges, int k) {
        const int n = edges.size() + 1;

        graph.resize(n);
        f.resize(n); g.resize(n);

        for (const auto &e : edges) {
            graph[e[0]].emplace_back(make_pair(e[1], e[2]));
            graph[e[1]].emplace_back(make_pair(e[0], e[2]));
        }

        solve(0, -1, k);

        return f[0];
    }
};