题目描述

有一个游戏，游戏由 n x n 个房间网格状排布组成。

给你一个大小为 n x n 的二位整数数组 fruits，其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。有三个小朋友 一开始 分别从角落房间 (0, 0)，(0, n - 1) 和 (n - 1, 0) 出发。

每一位小朋友都会 恰好 移动 n - 1 次，并到达房间 (n - 1, n - 1)：

• 从 (0, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达 (i + 1, j + 1)，(i + 1, j) 和 (i, j + 1) 房间之一（如果存在）。
• 从 (0, n - 1) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i + 1, j - 1)，(i + 1, j) 和 (i + 1, j + 1) 房间之一（如果存在）。
• 从 (n - 1, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i - 1, j + 1)，(i, j + 1) 和 (i + 1, j + 1) 房间之一（如果存在）。

当一个小朋友到达一个房间时，会把这个房间里所有的水果都收集起来。如果有两个或者更多小朋友进入同一个房间，只有一个小朋友能收集这个房间的水果。当小朋友离开一个房间时，这个房间里不会再有水果。

请你返回三个小朋友总共 最多 可以收集多少个水果。

样例

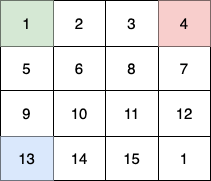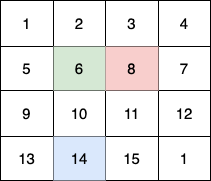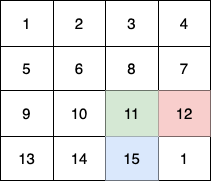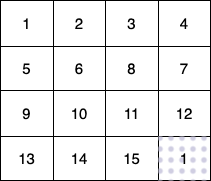
输入：fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]

输出：100

解释：

这个例子中：

第 1 个小朋友（绿色）的移动路径为 (0,0) -> (1,1) -> (2,2) -> (3, 3)。
第 2 个小朋友（红色）的移动路径为 (0,3) -> (1,2) -> (2,3) -> (3, 3)。
第 3 个小朋友（蓝色）的移动路径为 (3,0) -> (3,1) -> (3,2) -> (3, 3)。
他们总共能收集 1 + 6 + 11 + 1 + 4 + 8 + 12 + 13 + 14 + 15 = 100 个水果。

输入：fruits = [[1,1],[1,1]]

输出：4

解释：

这个例子中：

第 1 个小朋友移动路径为 (0,0) -> (1,1)。
第 2 个小朋友移动路径为 (0,1) -> (1,1)。
第 3 个小朋友移动路径为 (1,0) -> (1,1)。
他们总共能收集 1 + 1 + 1 + 1 = 4 个水果。

限制

• 2 <= n == fruits.length == fruits[i].length <= 1000
• 0 <= fruits[i][j] <= 1000

算法

(思维题，动态规划) $O(n^2)$

1. 注意到，第 1 个小朋友只有一条路，就是沿着对角线从 (0, 0) 走到 (n - 1, n - 1)，故先取对角线的数字之和。
2. 第 2 个和第 3 个小朋友除了会在对角线上重合外，其他地方都不会重合，但对角线上的数字已经被第 1 个小朋友取了，故第 2 个和第 3 个小朋友的路线一定是独立的。
3. 可以分别通过动态规划计算出两个人的最优路线，动态规划的思路类似于数字三角形，这里不再赘述。

时间复杂度

• 动态规划的状态数为 $O(n^2)$，转移时间为常数，故总时间复杂度为 $O(n^2)$。

空间复杂度

• 通过滚动数组优化，需要 $O(n)$ 的额外空间存储状态。

C++ 代码

const int N = 1010;

class Solution {
private:
    int f[2][N], g[2][N];

    inline int max(int x, int y) {
        return x > y ? x : y;
    }

public:
    int maxCollectedFruits(vector<vector<int>>& fruits) {
        const int n = fruits.size();
        int ans = 0;

        for (int i = 0; i < n; i++) {
            ans += fruits[i][i];
            fruits[i][i] = 0;
        }

        for (int j = 0; j < n; j++)
            f[0][j] = g[0][j] = INT_MIN;

        f[0][n - 1] = fruits[0][n - 1];
        g[0][n - 1] = fruits[n - 1][0];

        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++)
                f[i & 1][j] = g[i & 1][j] = INT_MIN;

            for (int j = n - 1; j >= max(n / 2, n - i - 1); j--) {
                f[i & 1][j] = max(
                    f[(i - 1) & 1][j - 1],
                    max(
                        f[(i - 1) & 1][j],
                        f[(i - 1) & 1][j + 1]
                    )
                ) + fruits[i][j];

                g[i & 1][j] = max(
                    g[(i - 1) & 1][j - 1],
                    max(
                        g[(i - 1) & 1][j],
                        g[(i - 1) & 1][j + 1]
                    )
                ) + fruits[j][i];
            }
        }

        ans += f[(n - 1) & 1][n - 1] + g[(n - 1) & 1][n - 1];

        return ans;
    }
};