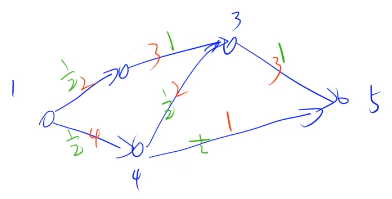
有向无环图
事件发生的期望的线性性E(aX+bY)=aE(X)+bE(Y)
f[i]:从i跳到N的期望长度
边界:f[N]=0
答案:f[1]
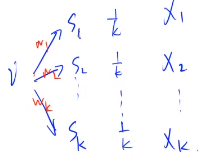
E(i)=E(1k(w1+x1)+1k(w2+x2)+…+1k(wk+xk))=1k(w1+E(x1))+1k(w2+E(x2))…+1k(wk+E(xk))=1k(w1+w2+…+wk)+1k(E(x1)+E(x2)+…+E(xk))f(i)=1k(w1+w2+…+wk)+1k(f(s1)+f(s2)+…+f(sk))=k∑i=11k(wi+f(si))
问题转化为按拓扑序从后往前推一遍
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dout[N];
double f[N];
void add(int a,int b,int c)
{
e[idx] = b,ne[idx] = h[a],w[idx]=c,h[a]=idx++;
}
double dp(int u)
{
if(f[u]>=0)return f[u];
f[u]=0;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
f[u]+=(w[i]+dp(j))/dout[u];
}
return f[u];
}
int main()
{
cin >> n >> m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
dout[a]++;
}
memset(f,-1,sizeof f);
printf("%.2lf\n",dp(1));
return 0;
}


大佬的期望写的很清晰,正好我不是很会
%%%
%%%
你这不是记忆化搜索写法?
蒟蒻刚学期望,问为什么期望要倒着求
期望路径长度从某个节点u出发可以分解为其所有邻接节点的期望值加上从u到这些邻接节点的边的权重。这意味着节点u的期望值依赖于其所有邻接节点的期望值。因此,我们需要先计算邻接节点的期望值,然后才能计算节点u的期望值
巨巨写得好