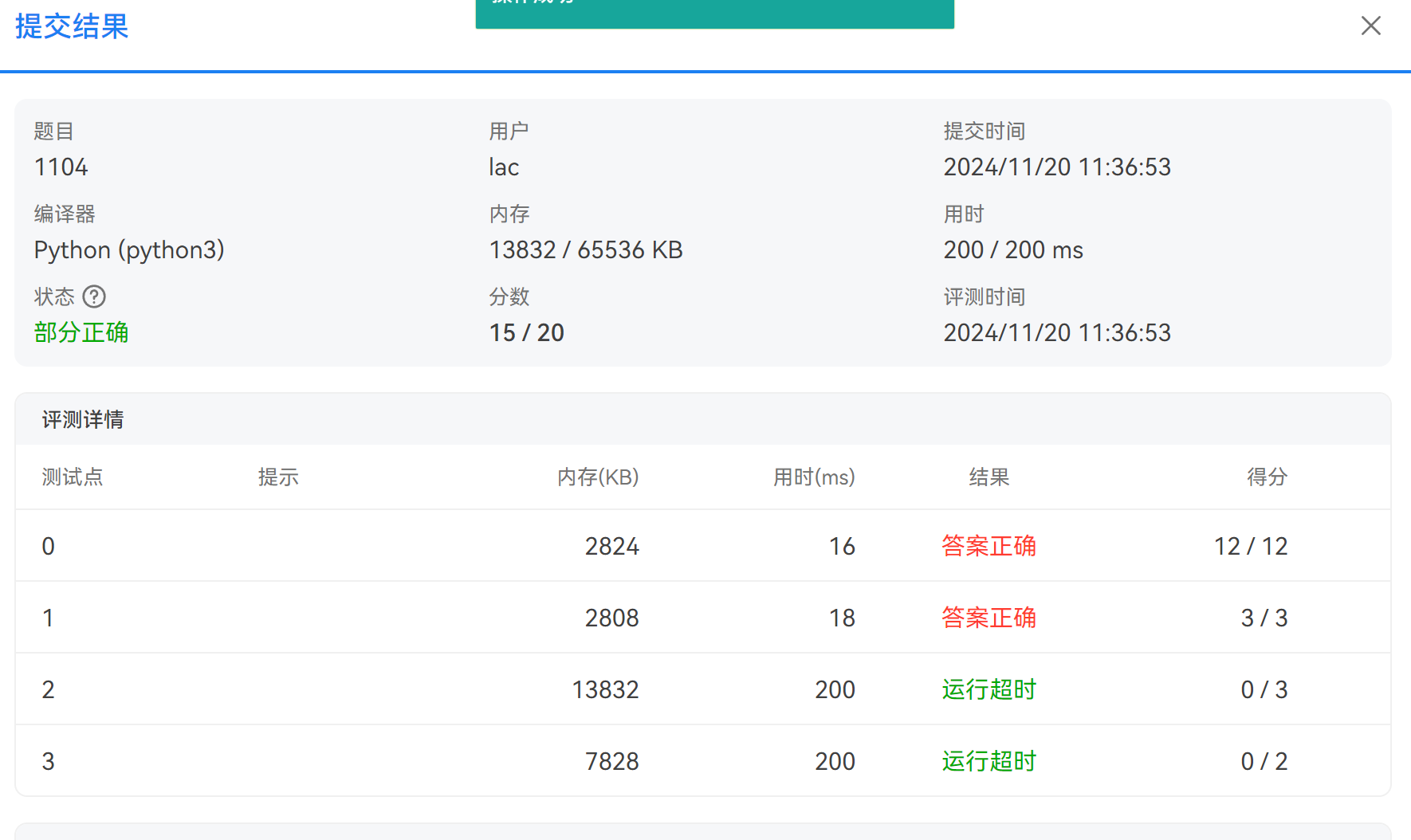
本题最容易想到的就是枚举数段的每一种情况，最容易想到的第一次循环是先枚举数段的长度，然后第二层循环计算该枚举的数段中各元素之和（算某区间元素之和可以使用前缀和，但本题即使是使用前缀和依然是在PAT超时了2个测试点）

n = int(input())
s = [0] * (n + 10)

i = 1
for x in map(float,input().split()):
    s[i] = s[i - 1] + x # 初始化前缀和数组
    i += 1


res = 0
for k in range(1,n + 1):# 枚举数段的长度，数段的长度可以是从1 ~ n
    i = 1
    j = i + k - 1
    while j <= n:
        res += s[j] - s[i - 1]
        i += 1
        j += 1

print(f'{res:.2f}')

因此本题需要优化：

统计下序列中每个数要加多少次，即看这个数在多少区间里面，区间有左端点和右端点，所以看左端点有多少种可能，右端点有多少种可能，再由乘法原理，最后区间个数为(左端点可能的个数 $\times$ 右端点可能的个数)。

==注意：此处的区间定义是以点定义的，即一个点也算一个区间==

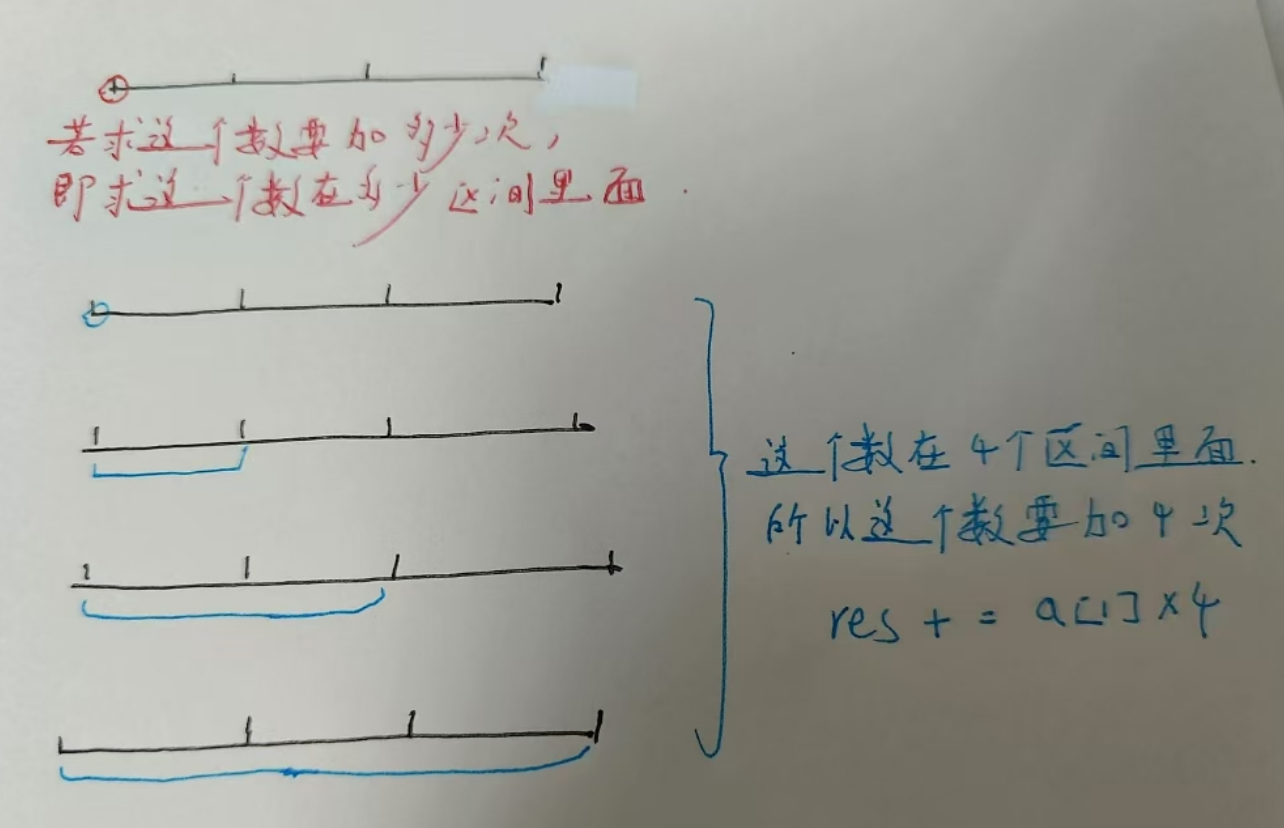
这个例子中$a[1]$的左端点为1个，即它自己，右端点为4个，所以总的区间个数为$1\times4=4$个

下面再看一个例子：

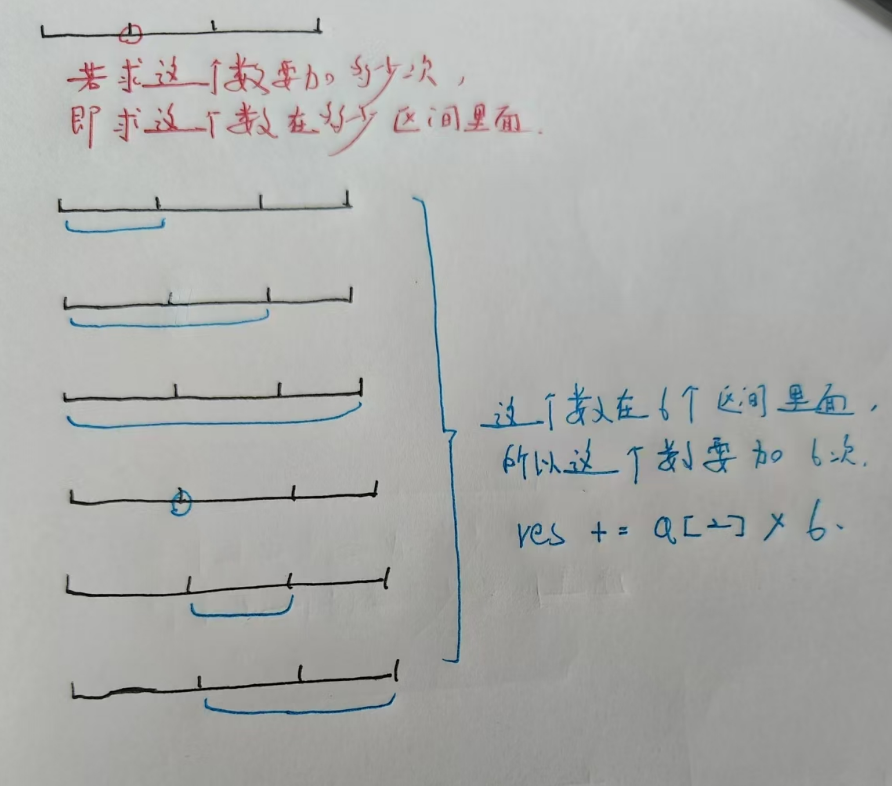
这个例子中$a[2]$的左端点为2个，右端点为3个，所以总的区间个数为$2 \times 3 = 6$个

再来看一个更一般的例子：

因此，最后总结一下做法：

设有序列$a[0],a[1],a[2],a[3]..a[n-1]$，对于序列中任意数$a[i]$,求$a[i]$这个数总共在多少区间里面，区间左端点可为0~i共i + 1个，右端点可为i ~ n - 1共n - i个，区间共$(i + 1) \times (n - i)$个，所以res += a[i] * (i + 1) * (n - i)

注意，以下代码是错误的，逻辑上以下代码并没有错误，但是错误的原因在于浮点数的精度不够

n = int(input())
a = [0] * (n + 10)

i = 1
for x in map(float,input().split()):
    a[i] = x
    i += 1

res = 0
for i in range(1,n + 1):
    res += a[i] * i * (n - i + 1)

print(f'{res:.2f}')

a = 123456789.12345678901234567890
print(a)
# 打印结果：123456789.12345679

对比以下：

123456789.12345678901234567890
123456789.12345679
# 可以看到，最后几位数字被舍去了，因为超出了浮点数的有效位数，py中float的有效位数为17位，可以看到18位的9向前四舍五入了，这就知道为什么上面的WA了，最后的输出比标准答案稍微大那么一点点

如果你需要更高的精度，可以使用Python的decimal模块，它提供了对十进制浮点运算的支持，可以指定任意精度。例如：

from decimal import Decimal, getcontext

"""
在Python的decimal模块中，getcontext()和prec的英文全称分别是：

getcontext() 的英文全称是 get the current context。这里的“context”指的是当前的十进制浮点运算环境，它包含了诸如精度、舍入模式等参数。通过getcontext()函数，你可以获取到这个环境对象，然后对其属性进行修改，以改变十进制浮点运算的行为。
prec 是 precision 的缩写，意为“精度”。在decimal模块的上下文中，prec表示的是十进制浮点数的有效数字位数。通过修改getcontext().prec的值，你可以设置全局的十进制浮点运算精度。
"""
# 设置全局精度
getcontext().prec = 50

a = Decimal('123456789.12345678901234567890')
print(a)

输出将会是：

123456789.12345678901234567890

在Python的decimal模块中，如果不显式设置全局精度（即不调用getcontext().prec = value），那么默认的精度是28位有效数字。这个默认值是根据IEEE 754双精度浮点数的精度以及decimal模块旨在提供比标准浮点数更高精度的目标来设定的。

需要注意的是，decimal模块的默认精度是全局的，一旦设置，就会影响该模块中所有后续的十进制浮点运算，直到再次更改它。因此，在进行特定精度的计算时，最好显式地设置所需的精度，以确保结果的准确性。

以下是一个例子，展示了在不设置全局精度的情况下，decimal.Decimal的默认行为：

from decimal import Decimal, getcontext

# 设置全局精度
# getcontext().prec = 50

a = Decimal('123456789.123456789012345678906898575')
b = Decimal('34.54')
print(a + b)
# 打印结果：123456823.6634567890123456789

设置全局精度的情况：

from decimal import Decimal, getcontext

# 设置全局精度
getcontext().prec = 50

a = Decimal('123456789.123456789012345678906898575')
b = Decimal('34.54')
print(a + b)
# 打印：123456823.663456789012345678906898575

本题完整代码：

# 引入 decimal 模块中的 Decimal 类，用于高精度浮点运算
from decimal import Decimal

n = int(input())
# 从标准输入读取一行由空格分隔的浮点数，将它们转换为 Decimal 类型，并存储在列表 a 中
a = list(map(Decimal, input().split()))

# 初始化总和变量 total_sum 为 Decimal 类型的 0，确保后续计算的高精度
total_sum = Decimal(0)

for i in range(n):
    total_sum += a[i] * (i + 1) * (n - i)

# 使用 quantize 方法将 total_sum 的值格式化为保留两位小数的 Decimal 类型
print(total_sum.quantize(Decimal('0.00')))