假设N可以表示成abcdefg，其中每一位代表一个0-9的数字。思路是枚举每一位上为1的数的个数，从高位开始枚举，把每一位出现的次数累加

那么如何计算某一位上为1的数的个数呢？

假如当前枚举到了从高到低的第4位，我们要计算从1~N中第4位为1的数字的个数，即d所在的数位，我们对d进行分情况讨论：

情况一：d < 1，即d = 0， 则前3位可以选择0 ~ abc - 1后3位可以选择0 ~ 999

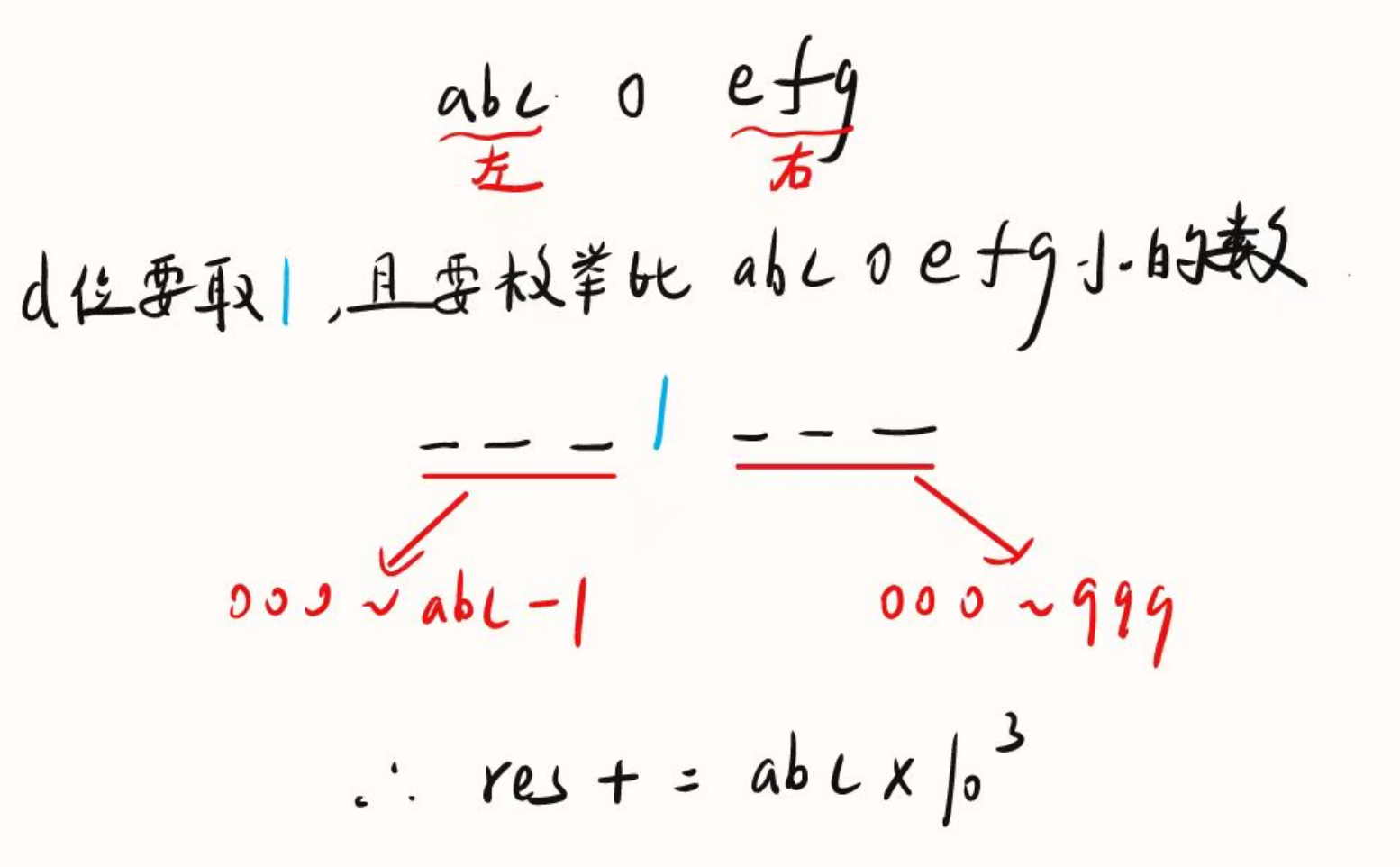
情况二：d = 1， 前3位可以选择abc后3位可以选择0 ~ efg。或者：前3位可以选择0 ~ abc - 1后3位可以选择0~999。

情况三：d > 1 前3位可以选择0 ~ abc后3位可以选择0-999

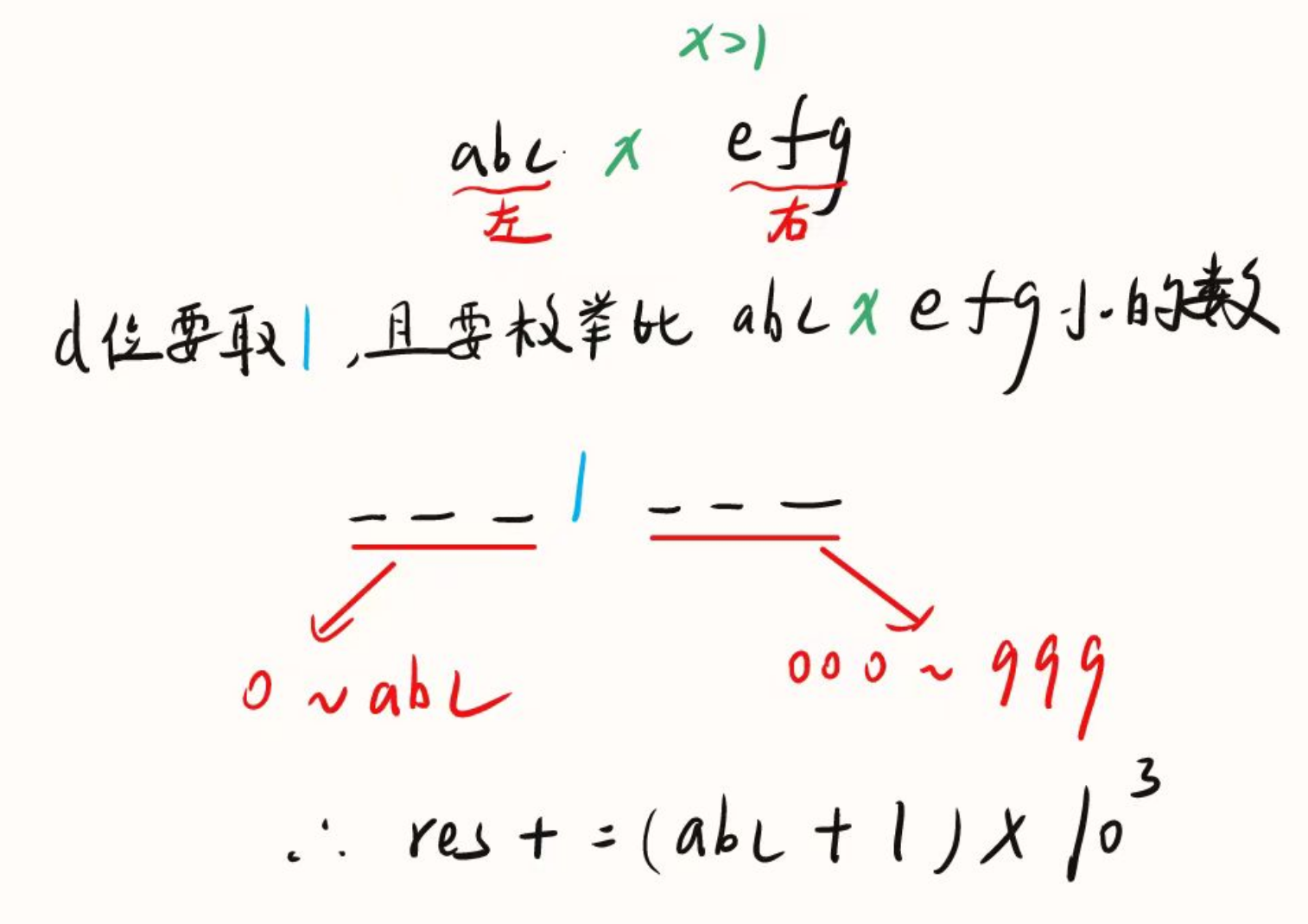
可以看到，枚举每一位时用到的数有abc, efg 以及10的k次方（k为从当前位的下一位到最低位的位数），在每次循环内部先将该三个变量预处理，在累加结果时方便直接调用

n = input()
res = 0
# 注意枚举时在边界时要特判一下，即枚举到最高位和最低位时，枚举到最高位没有left。枚举到最低位没有right。
# 这两种情况都令left和right为0，可以发现令它们为0时是正好满足的，可以带入验证
for i in range(len(n)):
    left,right,x = n[:i],n[i + 1:],int(n[i])
    k = len(right)
    if left:# 如果left不是空串
        left = int(left)
    else:# 如果是空串则置为0
        left = 0

    if right:# 如果right不是空串
        right = int(right)
    else:# 如果是空串则置为0
        right = 0

    if x == 0:# 情况一
        res += left * 10 ** k
    elif x == 1:# 情况二
        res += left * 10 ** k + right + 1
    elif x > 1:# 情况三
        res += (left + 1) * 10 ** k

print(res)