写在前面：本题按照y总思路，用图解模拟了样例的输入输出，以达到更好的理解,建议先看一遍y总视频

思路

算法核心思想

栈的核心作用是 逐步维护左边界的高度信息，并在遇到较高柱子时计算凹槽雨水量。
- 栈维护单调性：
- 栈存储的是柱子的 索引，且栈中的元素对应的柱子高度是 从高到低递减。
- 当新柱子（当前柱子）高度 height[i] 大于或等于 栈顶元素 height[stk.top()] 时：
- 栈顶元素 stk.top() 可以确定其左边和右边的柱子都比它高，因此可以计算凹槽面积。
- 雨水面积计算公式：
- 雨水的面积等于宽度乘以高度。
- 宽度：从当前柱子索引到栈顶柱子之间的距离。
- 高度：当前柱子和凹槽之间的最小高度差。

步骤

• 定义一个栈 stk 来存储柱子的索引。
• res 变量用于累加最终计算出的雨水总量。
• 遍历 height 数组中的每一个元素。
• last 用于记录当前柱子到前一个柱子之间的高度差，用来辅助计算当前能接住的雨水量。
• while 循环用于寻找左侧低于当前柱子的元素，计算其可以存储的雨水。
• 条件 1：stk.size() && height[stk.top()] <= height[i]：当前高度 height[i] 大于栈顶索引的高度。
  • 当前可以确定雨水积累高度，因为 height[stk.top()] 为凹槽。
• 雨水计算：
  • 计算 (height[stk.top()] - last) * (i - stk.top() - 1)，即雨水小矩形面积
  • 计算 (height[i] - last) * (i - stk.top() - 1) ，即雨水大矩形面积
  • i - stk.top() - 1 是左右柱子之间的宽度，height[stk.top()] - last 是凹槽深度。
• 如果栈中还有元素，说明 height[i] 比栈顶低。
• 此时再次计算雨水面积，左柱 stk.top() 仍能作为边界。
• 将当前索引压入栈，作为后续的高度边界参考。

图解样例

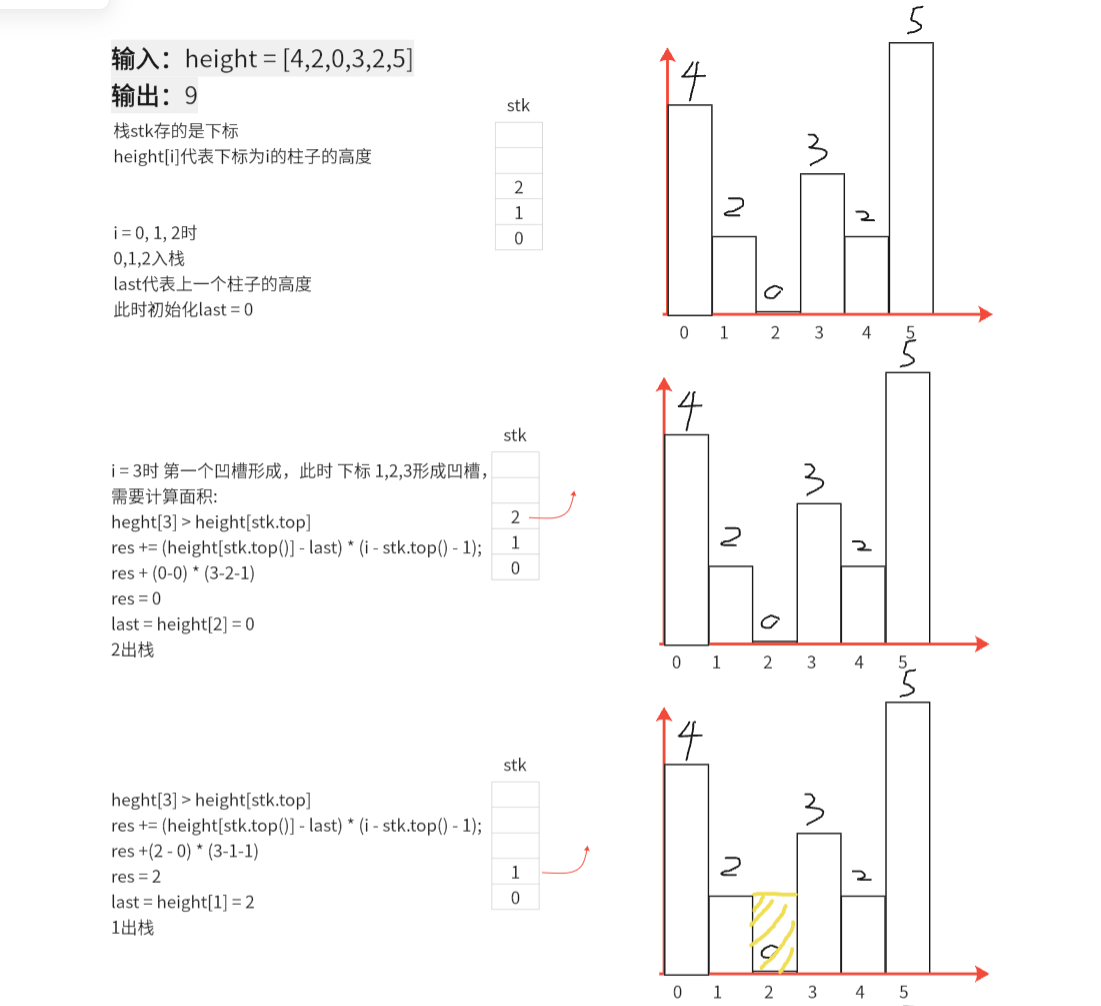
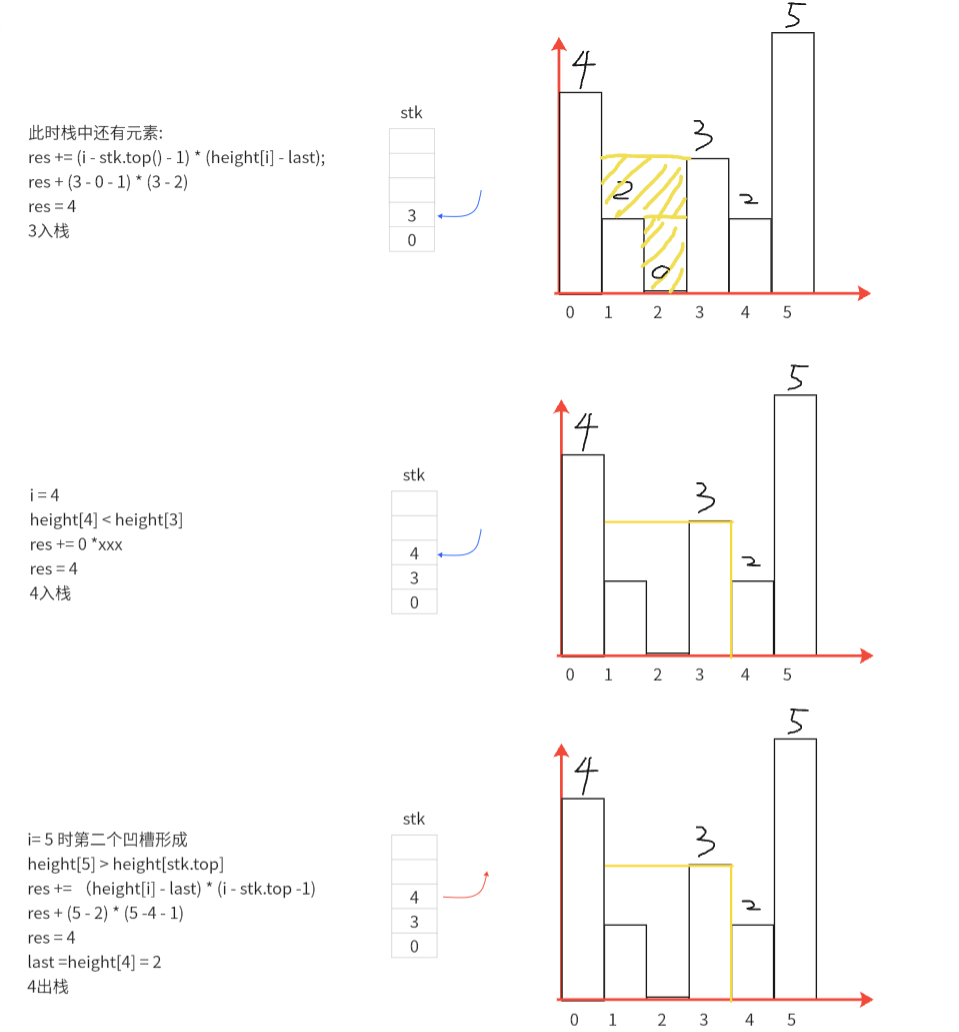
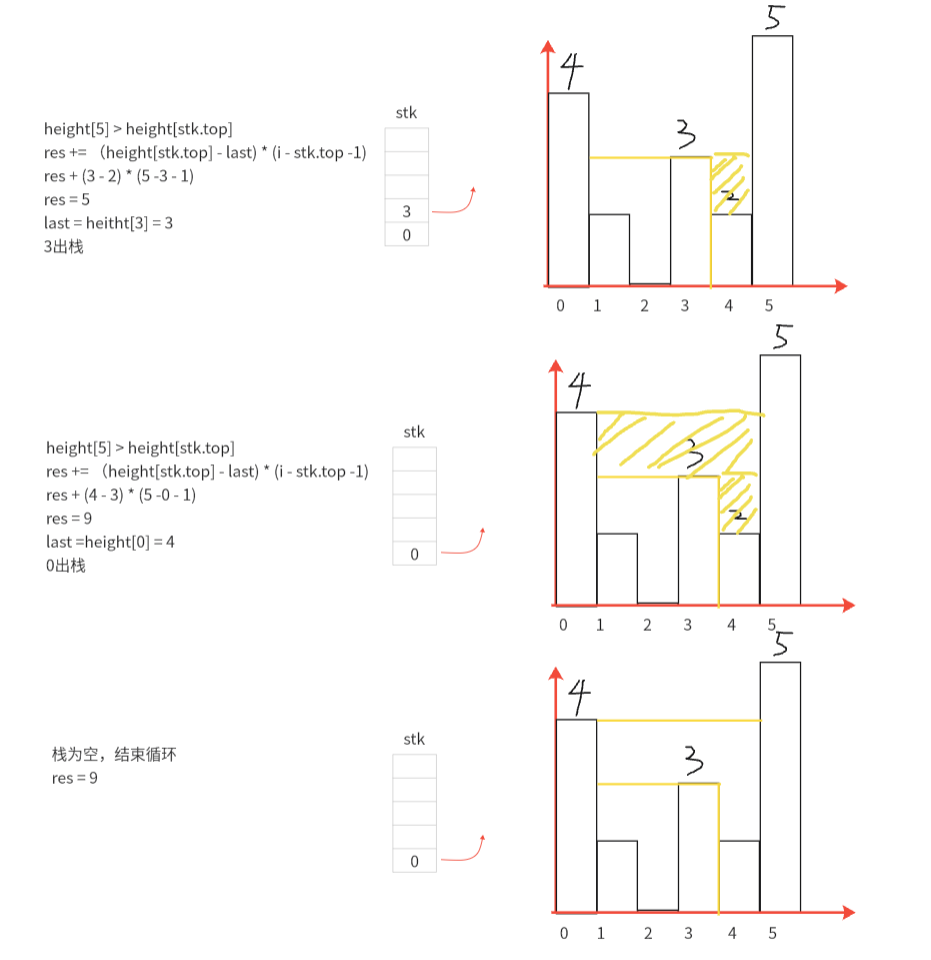
AC代码

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk; //存放的是下标
        int n = height.size();
        int res = 0;
        for(int i = 0 ;i < n ; i++)
        {
            int last = 0;//上一个柱子高度
            while(stk.size() && height[i] >= height[stk.top()])
            {
                res+=(height[stk.top()]- last) * (i - stk.top() - 1); //小矩形的面积
                last = height[stk.top()]; //更新last
                stk.pop();
            }
            if(stk.size())//如果栈中还有元素，计算大矩形得面积
            {
                res+=(height[i] - last) * (i - stk.top() - 1);
            }
            stk.push(i);
        }
        return res;
    }
};