题目描述

给你一棵 n 个节点且根节点为编号 0 的树，节点编号为 0 到 n - 1。这棵树用一个长度为 n 的数组 parent 表示，其中 parent[i] 是第 i 个节点的父亲节点的编号。由于节点 0 是根，parent[0] == -1。

给你一个长度为 n 的字符串 s，其中 s[i] 是节点 i 对应的字符。

对于节点编号从 1 到 n - 1 的每个节点 x，我们 同时 执行以下操作 一次：

• 找到距离节点 x 最近 的祖先节点 y，且 s[x] == s[y]。
• 如果节点 y 不存在，那么不做任何修改。
• 否则，将节点 x 与它父亲节点之间的边 删除，在 x 与 y 之间连接一条边，使 y 变为 x 新的父节点。

请你返回一个长度为 n 的数组 answer，其中 answer[i] 是 最终 树中，节点 i 为根的子树的 大小。

一个 子树 subtree 指的是节点 subtree 和它所有的后代节点。

样例

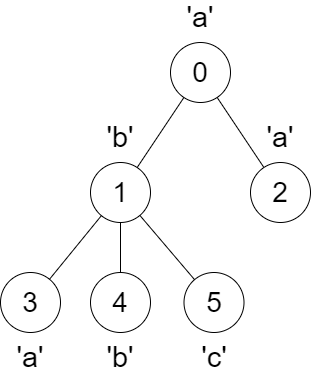
输入：parent = [-1,0,0,1,1,1], s = "abaabc"

输出：[6,3,1,1,1,1]

解释：

节点 3 的父节点从节点 1 变为节点 0。

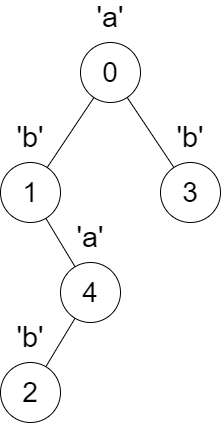
输入：parent = [-1,0,4,0,1], s = "abbba"

输出：[5,2,1,1,1]

解释：

以下变化会同时发生：

节点 4 的父节点从节点 1 变为节点 0 。
节点 2 的父节点从节点 4 变为节点 1 。

限制

• n == parent.length == s.length
• 1 <= n <= 10^5
• 对于所有的 i >= 1，都有 0 <= parent[i] <= n - 1。
• parent[0] == -1
• parent 表示一棵合法的树。
• s 只包含小写英文字母。

算法

(模拟，深度优先遍历) $O(n)$

1. 注意到最终树的结构与遍历的顺序无关，可以采用深度优先遍历的方式修改树的结构。
2. 第一次遍历过程中，自定向下记录每个字符最近一次出现的位置，并根据这个位置修改父节点。
3. 第二次遍历修改后的树，统计答案。

时间复杂度

• 每个节点遍历两次，遍历过程中每次仅需要常数的时间修改树结构，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储邻接表，递归的系统栈和答案。

C++ 代码

class Solution {
private:
    vector<vector<int>> graph;
    vector<int> prev;
    vector<int> ans;

    void dfs(int u, const string &s, vector<int> &parent) {
        int c = s[u] - 'a';
        int t = prev[c];
        if (t != -1)
            parent[u] = t;

        prev[c] = u;

        for (int v : graph[u])
            dfs(v, s, parent);

        prev[c] = t;
    }

    void solve(int u) {
        ans[u] = 1;
        for (int v : graph[u]) {
            solve(v);
            ans[u] += ans[v];
        }
    }

public:
    vector<int> findSubtreeSizes(vector<int>& parent, string s) {
        const int n = parent.size();

        graph.resize(n);
        for (int i = 1; i < n; i++)
            graph[parent[i]].push_back(i);

        prev.resize(26, -1);
        dfs(0, s, parent);

        graph.clear();

        graph.resize(n);
        for (int i = 1; i < n; i++)
            graph[parent[i]].push_back(i);

        ans.resize(n, 0);
        solve(0);

        return ans;
    }
};