题目描述

给你一棵 n 个节点的树，树的根节点为 0，n 个节点的编号为 0 到 n - 1。这棵树用一个长度为 n 的数组 parent 表示，其中 parent[i] 是节点 i 的父节点。由于节点 0 是根节点，所以 parent[0] == -1。

给你一个长度为 n 的字符串 s，其中 s[i] 是节点 i 对应的字符。

一开始你有一个空字符串 dfsStr，定义一个递归函数 dfs(int x)，它的输入是节点 x，并依次执行以下操作：

• 按照 节点编号升序 遍历 x 的每个孩子节点 y，并调用 dfs(y)。
• 将 字符 s[x] 添加到字符串 dfsStr 的末尾。

注意，所有递归函数 dfs 都共享全局变量 dfsStr 。

你需要求出一个长度为 n 的布尔数组 answer，对于 0 到 n - 1 的每一个下标 i，你需要执行以下操作：

• 清空字符串 dfsStr 并调用 dfs(i)。
• 如果结果字符串 dfsStr 是一个 回文串，answer[i] 为 true，否则 answer[i] 为 false。

请你返回字符串 answer。

样例

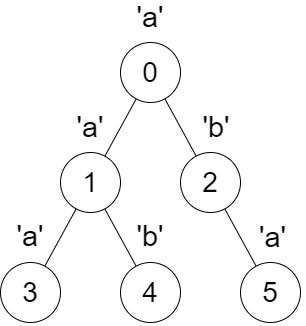
输入：parent = [-1,0,0,1,1,2], s = "aababa"

输出：[true,true,false,true,true,true]

解释：

调用 dfs(0)，得到字符串 dfsStr = "abaaba"，是一个回文串。
调用 dfs(1)，得到字符串dfsStr = "aba"，是一个回文串。
调用 dfs(2)，得到字符串dfsStr = "ab"，不 是回文串。
调用 dfs(3)，得到字符串dfsStr = "a"，是一个回文串。
调用 dfs(4)，得到字符串 dfsStr = "b"，是一个回文串。
调用 dfs(5)，得到字符串 dfsStr = "a"，是一个回文串。

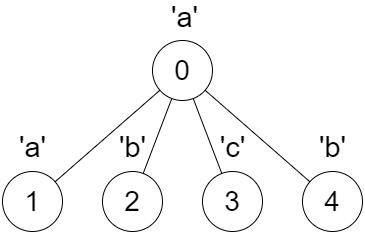
输入：parent = [-1,0,0,0,0], s = "aabcb"

输出：[true,true,true,true,true]

解释：

每一次调用 dfs(x) 都得到一个回文串。

限制

• n == parent.length == s.length
• 1 <= n <= 10^5
• 对于所有 i >= 1，都有 0 <= parent[i] <= n - 1。
• parent[0] == -1
• parent 表示一棵合法的树。
• s 只包含小写英文字母。

算法

(DFS 时间戳，字符串 RK 哈希) $O(n)$

1. 注意到，根节点遍历后得到的字符串中的子串包含了以所有节点开始遍历时得到的字符串。
2. 通过在 DFS 过程中引入时间戳，就可以得到每个节点在目标字符串上的开始位置和结束位置。
3. 然后对目标进行正反 RK 哈希，即前缀和后缀分别进行哈希。在校验时，判断区间正反的哈希值是否相同。
4. 采用双哈希的方式大幅减少碰撞的概率。

时间复杂度

• 建图的时间复杂度为 $O(n)$。
• DFS 的时间复杂度为 $O(n)$。
• 预处理哈希的时间复杂度为 $O(n)$。
• 单次判断回文的时间复杂度为常数。
• 故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储图，DFS 的系统栈，目标字符串，哈希数据结构和答案。

C++ 代码

#define ULL unsigned long long

const int M1 = 131, M2 = 13331;
const int N = 100010;

ULL pow1[N], pow2[N];

auto init = []{
    pow1[0] = pow2[0] = 1;

    for (int i = 1; i < N; i++) {
        pow1[i] = pow1[i - 1] * M1;
        pow2[i] = pow2[i - 1] * M2;
    }

    return 0;
}();

class Solution {
private:
    vector<vector<int>> graph;
    string target;
    vector<int> st, ed;
    int ts;

    void dfs(int u, int fa, const string &s) {
        st[u] = ts;

        for (int v : graph[u])
            if (v != fa)
                dfs(v, u, s);

        ed[u] = ts++;
        target += s[u];
    }

    bool check(int l, int r,
        const vector<ULL> &h, const vector<ULL> &hr, const ULL *pow
    ) {
        int len = r - l + 1;
        return h[r] - h[l - 1] * pow[len] == hr[l] - hr[r + 1] * pow[len];
    }

public:
    vector<bool> findAnswer(vector<int>& parent, string s) {
        const int n = parent.size();

        graph.resize(n);
        for (int i = 1; i < n; i++)
            graph[parent[i]].push_back(i);

        for (int i = 0; i < n; i++)
            sort(graph[i].begin(), graph[i].end());

        st.resize(n); ed.resize(n);

        ts = 1;
        dfs(0, -1, s);

        vector<ULL> h1(n + 1), h2(n + 1);
        h1[0] = h2[0] = 0;
        for (int i = 1; i <= n; i++) {
            h1[i] = h1[i - 1] * M1 + target[i - 1] - 'a' + 1;
            h2[i] = h2[i - 1] * M2 + target[i - 1] - 'a' + 1;
        }

        vector<ULL> hr1(n + 2), hr2(n + 2);
        hr1[n + 1] = hr2[n + 1] = 0;
        for (int i = n; i >= 1; i--) {
            hr1[i] = hr1[i + 1] * M1 + target[i - 1] - 'a' + 1;
            hr2[i] = hr2[i + 1] * M2 + target[i - 1] - 'a' + 1;
        }

        vector<bool> ans(n);
        for (int i = 0; i < n; i++)
            ans[i] = check(st[i], ed[i], h1, hr1, pow1) && 
                check(st[i], ed[i], h2, hr2, pow2);

        return ans;
    }
};